ഗുരുത്വതരംഗങ്ങളെ കണ്ടെത്തിയ വാർത്ത കഴിഞ്ഞ ദിവസം ശാസ്ത്രലോകത്തെ ഇളക്കി മറിച്ചത് എല്ലാവരും അറിഞ്ഞല്ലോ. ആ സമയത്ത് മാധ്യമങ്ങളും സോഷ്യൽ മീഡിയ ന്യൂസ് ഫീഡും ഒക്കെ കണ്ട് ഇന്നസെന്റിനെപ്പോലെ "എന്തിനാ എല്ലാവരും പടക്കം പൊട്ടിക്കണേ? ഇന്നെന്താ വിഷുവാ?" എന്ന ഭാവത്തിൽ നിന്നവർക്കും "എന്തോ വല്യ സംഭവമാണ്" എന്നുമാത്രം മനസിലാക്കി വണ്ടറടിച്ച് നിന്നവർക്കും വേണ്ടി സംഗതിയുടെ ഗുട്ടൻസ് വിശദീകരിക്കാനുള്ള ഒരു ശ്രമമാണ് നടത്താൻ പോകുന്നത്. ഇത്തിരി നീളമുണ്ട്. ക്ഷമിക്കണം, ഇതിലും ചുരുക്കിയാൽ പറഞ്ഞിട്ട് കാര്യമുണ്ടാകില്ല.
ഗുരുത്വാകർഷണ ബലം- ന്യൂട്ടന് പറയാൻ കഴിയാത്തത്
ഗുരുത്വതരംഗങ്ങൾ എന്താണെന്ന് വിശദീകരിക്കുന്നതിന് മുൻപ്, ആ സങ്കല്പത്തിന്റെ വരവ് ഏത് റൂട്ടിലൂടെയാണെന്ന് മനസിലാക്കേണ്ടതുണ്ട്. ഗുരുത്വാകർഷണം ഐസക് ന്യൂട്ടന്റെ കണ്ടുപിടുത്തമാണെന്ന് അറിയാമല്ലോ അല്ലേ? ന്യൂട്ടൻ, പിണ്ഡം (mass) ഉള്ള ഏത് രണ്ട് വസ്തുക്കളും പരസ്പരം ആകർഷിക്കുന്നു എന്ന് സിദ്ധാന്തിച്ചു. ആ ആകർഷണബലത്തിന്റെ അളവ് കണക്കാക്കാനുള്ള ഒരു സമവാക്യവും അദ്ദേഹം രൂപീകരിച്ചു.
F = G M1 M2/r²
ഇവിടെ M1, M2 എന്നിവ പരസ്പരം ഗുരുത്വാകർഷണം ചെലുത്തുന്ന രണ്ട് വസ്തുക്കളുടെ പിണ്ഡങ്ങളാണ്. r അവയ്ക്കിടയിലെ ദൂരവും. G എന്നത് പ്രപഞ്ചത്തിലെല്ലായിടത്തും ഒരേ മൂല്യമുള്ള ഒരു സംഖ്യയാണ്, ഗ്രാവിറ്റേഷണൽ കോൺസ്റ്റന്റ് എന്ന് വിളിക്കും. ഈ സമവാക്യം ഭൗതികശാസ്ത്രത്തിന്റെ നെടുംതൂണായി മാറിയ ഒന്നാണ്. പലരും കരുതിയിരിക്കുന്നത് പോലെ ആപ്പിൾ താഴേയ്ക്ക് വീഴുന്നത് ഭൂമി താഴേയ്ക്ക് വലിക്കുന്നതുകൊണ്ടാണ് എന്ന് കണ്ടുപിടിച്ചതുകൊണ്ടല്ല ന്യൂട്ടനെ എല്ലാവരും പുകഴ്ത്തുന്നത്. ആപ്പിളിനെ താഴേയ്ക്ക് വലിക്കുന്ന അതേ ബലം വെച്ച് ഗ്രഹങ്ങളും ഉപഗ്രഹങ്ങളും ഉൾപ്പടെ സൗരയൂഥത്തിലെ മുഴുവൻ വസ്തുക്കളുടേയും മാത്രമല്ല, ബോധ്യപ്പെടാവുന്ന എല്ലാ ചലനങ്ങളേയും കിറുകൃത്യമായി വിശദീകരിച്ചതിനാണ്. മേൽപ്പറഞ്ഞ സമവാക്യം കാഴ്ചയ്ക്ക് ലളിതമെന്ന് തോന്നുമെങ്കിലും ഇതിന്റെ പ്രയോഗക്ഷമത അപാരമായിരുന്നു. സമവാക്യം ലളിതമാണെന്നത് തോന്നലല്ല,സത്യം തന്നെയാണ്. പക്ഷേ അഞ്ച് വസ്തുക്കളെ ഒരുമിച്ച് പരിഗണിക്കുമ്പോൾ ഇവയിൽ ഓരോ ജോഡിയും പരസ്പരം ആകർഷിക്കുന്നുണ്ട് എന്നോർക്കണം. അപ്പോൾ സാഹചര്യം സങ്കീർണമാകുന്നു, അതിനനുസരിച്ച് കണക്കുകൂട്ടലും ബുദ്ധിമുട്ടുള്ളതാകുന്നു. പക്ഷേ അപ്പോഴും അടിസ്ഥാനം ലളിതമായ ആ സമവാക്യം തന്നെയാണ്.
സങ്കീർണതയ്ക്ക് ഉദാഹരണം പറഞ്ഞാൽ, സൗരയൂഥത്തിൽ സൂര്യന്റെ ആകർഷണം കാരണമാണ് ഗ്രഹങ്ങൾ അതിന് ചുറ്റും കറങ്ങുന്നത് എന്നറിയാമായിരിക്കും. പക്ഷേ സൂര്യനും ഗ്രഹങ്ങളും തമ്മിൽ മാത്രമല്ല, ഗ്രഹങ്ങൾ തമ്മിൽത്തമ്മിലും ആകർഷണമുണ്ട്. സൂര്യനേയും ഭൂമിയേയും M1, M2 ആയി പരിഗണിച്ച് സമവാക്യം ഉപയോഗിച്ചാൽ ഭൂമിയുടെ കൃത്യമായ സഞ്ചാരപഥം കണക്കാക്കാനാകില്ല. മറ്റ് ഗ്രഹങ്ങൾ ചെലുത്തുന്ന ആകർഷണം കൂടി പരിഗണിച്ചാലേ അതിന് സാധിയ്ക്കൂ. പണ്ട് സൗരയൂഥത്തിൽ വെറും ഏഴ് ഗ്രഹങ്ങളെക്കുറിച്ച് മാത്രം അറിവുണ്ടായിരുന്ന കാലത്ത്, യുറാനസിന്റെ (അന്നത്തെ കണക്കിൽ ഏറ്റവും അകലെയുള്ള ഗ്രഹം) ചലനത്തെ വിശദീകരിക്കാൻ ശ്രമിക്കവേ കണക്കുകൂട്ടലുകളുമായി ചില പൊരുത്തക്കേടുകൾ കാണപ്പെട്ടു. പലവിധ ചിന്തകൾക്കൊടുവിൽ, ഇനിയുമറിയാത്ത ഒരു ഗ്രഹത്തിന്റെ സ്വാധീനം കാരണമാകുമോ യുറാനസിന്റെ സഞ്ചാരപഥം മാറുന്നത് എന്ന സംശയം വന്നു. അങ്ങനെ യുറാനസിനും അപ്പുറം മറ്റൊരു ഗ്രഹത്തെ സങ്കല്പിച്ച് നടത്തിയ കണക്കുകൂട്ടലുകൾ നിരീക്ഷണവുമായി ഒത്തുവന്നപ്പോൾ അതേ കണക്കുകൂട്ടലുകൾ പ്രവചിച്ച സ്ഥാനത്തേയ്ക്ക് തിരിച്ച ടെലിസ്കോപ്പിലാണ് നെപ്റ്റ്യൂൺ ആദ്യമായി കാണപ്പെട്ടത്. അതായത്, നെപ്റ്റ്യൂണിനെ നമ്മൾ കണ്ട് തിരിച്ചറിഞ്ഞതല്ല. ന്യൂട്ടന്റെ സമവാക്യങ്ങൾ നമുക്ക് ചൂണ്ടിക്കാണിച്ച് തന്നതാണ്.
ഗുരുത്വാകർഷണ ബലം- ന്യൂട്ടന് പറയാൻ കഴിയാത്തത്
ഗുരുത്വതരംഗങ്ങൾ എന്താണെന്ന് വിശദീകരിക്കുന്നതിന് മുൻപ്, ആ സങ്കല്പത്തിന്റെ വരവ് ഏത് റൂട്ടിലൂടെയാണെന്ന് മനസിലാക്കേണ്ടതുണ്ട്. ഗുരുത്വാകർഷണം ഐസക് ന്യൂട്ടന്റെ കണ്ടുപിടുത്തമാണെന്ന് അറിയാമല്ലോ അല്ലേ? ന്യൂട്ടൻ, പിണ്ഡം (mass) ഉള്ള ഏത് രണ്ട് വസ്തുക്കളും പരസ്പരം ആകർഷിക്കുന്നു എന്ന് സിദ്ധാന്തിച്ചു. ആ ആകർഷണബലത്തിന്റെ അളവ് കണക്കാക്കാനുള്ള ഒരു സമവാക്യവും അദ്ദേഹം രൂപീകരിച്ചു.
F = G M1 M2/r²
ഇവിടെ M1, M2 എന്നിവ പരസ്പരം ഗുരുത്വാകർഷണം ചെലുത്തുന്ന രണ്ട് വസ്തുക്കളുടെ പിണ്ഡങ്ങളാണ്. r അവയ്ക്കിടയിലെ ദൂരവും. G എന്നത് പ്രപഞ്ചത്തിലെല്ലായിടത്തും ഒരേ മൂല്യമുള്ള ഒരു സംഖ്യയാണ്, ഗ്രാവിറ്റേഷണൽ കോൺസ്റ്റന്റ് എന്ന് വിളിക്കും. ഈ സമവാക്യം ഭൗതികശാസ്ത്രത്തിന്റെ നെടുംതൂണായി മാറിയ ഒന്നാണ്. പലരും കരുതിയിരിക്കുന്നത് പോലെ ആപ്പിൾ താഴേയ്ക്ക് വീഴുന്നത് ഭൂമി താഴേയ്ക്ക് വലിക്കുന്നതുകൊണ്ടാണ് എന്ന് കണ്ടുപിടിച്ചതുകൊണ്ടല്ല ന്യൂട്ടനെ എല്ലാവരും പുകഴ്ത്തുന്നത്. ആപ്പിളിനെ താഴേയ്ക്ക് വലിക്കുന്ന അതേ ബലം വെച്ച് ഗ്രഹങ്ങളും ഉപഗ്രഹങ്ങളും ഉൾപ്പടെ സൗരയൂഥത്തിലെ മുഴുവൻ വസ്തുക്കളുടേയും മാത്രമല്ല, ബോധ്യപ്പെടാവുന്ന എല്ലാ ചലനങ്ങളേയും കിറുകൃത്യമായി വിശദീകരിച്ചതിനാണ്. മേൽപ്പറഞ്ഞ സമവാക്യം കാഴ്ചയ്ക്ക് ലളിതമെന്ന് തോന്നുമെങ്കിലും ഇതിന്റെ പ്രയോഗക്ഷമത അപാരമായിരുന്നു. സമവാക്യം ലളിതമാണെന്നത് തോന്നലല്ല,സത്യം തന്നെയാണ്. പക്ഷേ അഞ്ച് വസ്തുക്കളെ ഒരുമിച്ച് പരിഗണിക്കുമ്പോൾ ഇവയിൽ ഓരോ ജോഡിയും പരസ്പരം ആകർഷിക്കുന്നുണ്ട് എന്നോർക്കണം. അപ്പോൾ സാഹചര്യം സങ്കീർണമാകുന്നു, അതിനനുസരിച്ച് കണക്കുകൂട്ടലും ബുദ്ധിമുട്ടുള്ളതാകുന്നു. പക്ഷേ അപ്പോഴും അടിസ്ഥാനം ലളിതമായ ആ സമവാക്യം തന്നെയാണ്.
സങ്കീർണതയ്ക്ക് ഉദാഹരണം പറഞ്ഞാൽ, സൗരയൂഥത്തിൽ സൂര്യന്റെ ആകർഷണം കാരണമാണ് ഗ്രഹങ്ങൾ അതിന് ചുറ്റും കറങ്ങുന്നത് എന്നറിയാമായിരിക്കും. പക്ഷേ സൂര്യനും ഗ്രഹങ്ങളും തമ്മിൽ മാത്രമല്ല, ഗ്രഹങ്ങൾ തമ്മിൽത്തമ്മിലും ആകർഷണമുണ്ട്. സൂര്യനേയും ഭൂമിയേയും M1, M2 ആയി പരിഗണിച്ച് സമവാക്യം ഉപയോഗിച്ചാൽ ഭൂമിയുടെ കൃത്യമായ സഞ്ചാരപഥം കണക്കാക്കാനാകില്ല. മറ്റ് ഗ്രഹങ്ങൾ ചെലുത്തുന്ന ആകർഷണം കൂടി പരിഗണിച്ചാലേ അതിന് സാധിയ്ക്കൂ. പണ്ട് സൗരയൂഥത്തിൽ വെറും ഏഴ് ഗ്രഹങ്ങളെക്കുറിച്ച് മാത്രം അറിവുണ്ടായിരുന്ന കാലത്ത്, യുറാനസിന്റെ (അന്നത്തെ കണക്കിൽ ഏറ്റവും അകലെയുള്ള ഗ്രഹം) ചലനത്തെ വിശദീകരിക്കാൻ ശ്രമിക്കവേ കണക്കുകൂട്ടലുകളുമായി ചില പൊരുത്തക്കേടുകൾ കാണപ്പെട്ടു. പലവിധ ചിന്തകൾക്കൊടുവിൽ, ഇനിയുമറിയാത്ത ഒരു ഗ്രഹത്തിന്റെ സ്വാധീനം കാരണമാകുമോ യുറാനസിന്റെ സഞ്ചാരപഥം മാറുന്നത് എന്ന സംശയം വന്നു. അങ്ങനെ യുറാനസിനും അപ്പുറം മറ്റൊരു ഗ്രഹത്തെ സങ്കല്പിച്ച് നടത്തിയ കണക്കുകൂട്ടലുകൾ നിരീക്ഷണവുമായി ഒത്തുവന്നപ്പോൾ അതേ കണക്കുകൂട്ടലുകൾ പ്രവചിച്ച സ്ഥാനത്തേയ്ക്ക് തിരിച്ച ടെലിസ്കോപ്പിലാണ് നെപ്റ്റ്യൂൺ ആദ്യമായി കാണപ്പെട്ടത്. അതായത്, നെപ്റ്റ്യൂണിനെ നമ്മൾ കണ്ട് തിരിച്ചറിഞ്ഞതല്ല. ന്യൂട്ടന്റെ സമവാക്യങ്ങൾ നമുക്ക് ചൂണ്ടിക്കാണിച്ച് തന്നതാണ്.
ഇങ്ങനെ നിരവധി വിജയങ്ങളുമായി രണ്ട് നൂറ്റാണ്ടുകളോളം ന്യൂട്ടന്റെ ഗുരുത്വാകർഷണ നിയമം ഭൗതികശാസ്ത്രലോകത്തെ അടക്കിവാണു. ഇന്നും ബഹിരാകാശ യാത്രകളിൽ പോലും ന്യൂട്ടന്റെ നിയമങ്ങൾ പ്രയോഗിക്കപ്പെടുന്നു. അപ്പോളോ-8 ദൗത്യത്തിലെ യാത്രികനായിരുന്ന വില്യം സാൻഡേഴ്സിന്റെ, പ്രശസ്തമായ ഒരു വാചകമുണ്ട്. മടക്കയാത്രയ്ക്കിടെ, ഇപ്പോളാരാണ് പേടകം ഓടിക്കുന്നത് എന്ന ഒരു കുട്ടിയുടെ ചോദ്യത്തിന് അദ്ദേഹം പറഞ്ഞ മറുപടി- "ഡ്രൈവിങ് ഏതാണ്ട് മുഴുവനായും ഐസക് ന്യൂട്ടനാണ് ചെയ്യുന്നത്" എന്നായിരുന്നു ("I think Isaac Newton is doing most of the driving now") ബഹിരാകാശ പേടകം ഗുരുത്വനിയമങ്ങൾ മാത്രമനുസരിച്ച് സ്വയം നീങ്ങുകയാണ് എന്നാണദ്ദേഹം ഉദ്ദേശിച്ചത്.
എന്നാൽ കാലങ്ങൾക്ക് ശേഷം ന്യൂട്ടന്റെ സിദ്ധാന്തം പൊളിച്ചെഴുതേണ്ടി വന്നു. തന്റെ സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം (General Theory of Relativity) വഴി ആൽബർട്ട് ഐൻസ്റ്റൈൻ ആണ് ആ ദൗത്യം നിർവഹിച്ചത്. ഇത്രയധികം വിജയകരമായ ന്യൂട്ടന്റെ സിദ്ധാന്തം പരിഷ്കരിക്കേണ്ട ആവശ്യം എന്തായിരുന്നു?
പൊതുവേ വൻ വിജയമെന്ന് കരുതപ്പെട്ടിരുന്നു എങ്കിലും, ഒരു പ്രത്യേക കാര്യത്തിൽ ന്യൂട്ടന്റെ സമവാക്യങ്ങൾ പ്രവചിക്കുന്ന ചില ചലനങ്ങൾ നിരീക്ഷണങ്ങളിൽ നിന്ന് വ്യതിചലിക്കുന്നത് ശ്രദ്ധയിൽ പെട്ടിരുന്നു. ബുധഗ്രഹത്തിന്റെ ഓർബിറ്റായിരുന്നു അത്. യുറാനസിന്റെ ഓർബിറ്റിലെ പന്തികേട് വിശദീകരിക്കാനായി മറ്റൊരു ഗ്രഹത്തിന്റെ സാന്നിദ്ധ്യം പ്രവചിച്ച കാര്യം നേരത്തേ നമ്മൾ പറഞ്ഞു. നെപ്റ്റ്യൂണിനെ കണ്ടതോടെ ന്യൂട്ടൻ നിയമത്തിന്റെ അക്കൗണ്ടിൽ ആ ക്രെഡിറ്റ് രേഖപ്പെടുത്തുകയും ചെയ്തു. ഇതുപോലെ ബുധന്റെ ഓർബിറ്റിനെ സ്വാധീനിക്കും വിധം സൂര്യനും ബുധനും ഇടയിൽ മറ്റൊരു ഗ്രഹമുണ്ടാകാം എന്നൊരു പ്രവചനം ചില ശാസ്ത്രജ്ഞർ നടത്തുകയുണ്ടായി. നെപ്റ്റ്യൂണിനെ പ്രവചിച്ച ലെ വെര്യർ എന്ന ശാസ്ത്രജ്ഞൻ തന്നെയാണ് അതിന് നേതൃത്വം കൊടുത്തത്. അതിന് അദ്ദേഹം വൾക്കൻ എന്ന് പേരിടുകയും ചെയ്തു. അതിന് ശേഷം പലയിടത്തുനിന്നായി പലരും വൾക്കനെ ശരിയ്ക്കും കണ്ടെത്തി എന്ന അവകാശവാദങ്ങളുമായി മുന്നോട്ട് വന്നു. പക്ഷേ അവയെല്ലാം തന്നെ പല രീതിയിലും സംശയം തോന്നിപ്പിക്കുന്ന വിധമുള്ള റിപ്പോർട്ടുകളായിരുന്നു. 1877-ൽ ലെ വെര്യർ മരിക്കുന്നതുവരെയും താൻ ഒരു പുതിയ ഗ്രഹത്തെക്കൂടി കണ്ടെത്തി എന്ന ധാരണയിലായിരുന്നു അദ്ദേഹം. അതിന് ശേഷവും പരക്കെ വൾക്കന് വേണ്ടിയുള്ള തിരച്ചിലുകൾ ജ്യോതിശാസ്ത്രജ്ഞർ തുടർന്നെങ്കിലും ആരും എങ്ങുനിന്നും വൾക്കനെ കണ്ടില്ല.
1915-ൽ ഐൻസ്റ്റൈന്റെ സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം വന്നതോടെ, മറ്റൊരു ഗ്രഹത്തിന്റെ സാന്നിദ്ധ്യമില്ലാതെ തന്നെ ബുധന്റെ ഓർബിറ്റ് കൃത്യമായി വിശദീകരിക്കാം എന്ന് തെളിഞ്ഞു. അതിന് മറ്റൊരു ഗൗരവകരമായ അർത്ഥം കൂടി ഉണ്ടായിരുന്നു. ന്യൂട്ടന്റെ സിദ്ധാന്തങ്ങളിൽ എവിടെയോ എന്തൊക്കെയോ പോരായ്മകളുണ്ട്!
അതെ, അതുണ്ട്. തത്കാലം അത് തിരിച്ചറിയാനുള്ള എളുപ്പത്തിന് നമുക്കൊരു ചിന്താപരീക്ഷണം നടത്തിനോക്കാം.
പൊതുവേ വൻ വിജയമെന്ന് കരുതപ്പെട്ടിരുന്നു എങ്കിലും, ഒരു പ്രത്യേക കാര്യത്തിൽ ന്യൂട്ടന്റെ സമവാക്യങ്ങൾ പ്രവചിക്കുന്ന ചില ചലനങ്ങൾ നിരീക്ഷണങ്ങളിൽ നിന്ന് വ്യതിചലിക്കുന്നത് ശ്രദ്ധയിൽ പെട്ടിരുന്നു. ബുധഗ്രഹത്തിന്റെ ഓർബിറ്റായിരുന്നു അത്. യുറാനസിന്റെ ഓർബിറ്റിലെ പന്തികേട് വിശദീകരിക്കാനായി മറ്റൊരു ഗ്രഹത്തിന്റെ സാന്നിദ്ധ്യം പ്രവചിച്ച കാര്യം നേരത്തേ നമ്മൾ പറഞ്ഞു. നെപ്റ്റ്യൂണിനെ കണ്ടതോടെ ന്യൂട്ടൻ നിയമത്തിന്റെ അക്കൗണ്ടിൽ ആ ക്രെഡിറ്റ് രേഖപ്പെടുത്തുകയും ചെയ്തു. ഇതുപോലെ ബുധന്റെ ഓർബിറ്റിനെ സ്വാധീനിക്കും വിധം സൂര്യനും ബുധനും ഇടയിൽ മറ്റൊരു ഗ്രഹമുണ്ടാകാം എന്നൊരു പ്രവചനം ചില ശാസ്ത്രജ്ഞർ നടത്തുകയുണ്ടായി. നെപ്റ്റ്യൂണിനെ പ്രവചിച്ച ലെ വെര്യർ എന്ന ശാസ്ത്രജ്ഞൻ തന്നെയാണ് അതിന് നേതൃത്വം കൊടുത്തത്. അതിന് അദ്ദേഹം വൾക്കൻ എന്ന് പേരിടുകയും ചെയ്തു. അതിന് ശേഷം പലയിടത്തുനിന്നായി പലരും വൾക്കനെ ശരിയ്ക്കും കണ്ടെത്തി എന്ന അവകാശവാദങ്ങളുമായി മുന്നോട്ട് വന്നു. പക്ഷേ അവയെല്ലാം തന്നെ പല രീതിയിലും സംശയം തോന്നിപ്പിക്കുന്ന വിധമുള്ള റിപ്പോർട്ടുകളായിരുന്നു. 1877-ൽ ലെ വെര്യർ മരിക്കുന്നതുവരെയും താൻ ഒരു പുതിയ ഗ്രഹത്തെക്കൂടി കണ്ടെത്തി എന്ന ധാരണയിലായിരുന്നു അദ്ദേഹം. അതിന് ശേഷവും പരക്കെ വൾക്കന് വേണ്ടിയുള്ള തിരച്ചിലുകൾ ജ്യോതിശാസ്ത്രജ്ഞർ തുടർന്നെങ്കിലും ആരും എങ്ങുനിന്നും വൾക്കനെ കണ്ടില്ല.
1915-ൽ ഐൻസ്റ്റൈന്റെ സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം വന്നതോടെ, മറ്റൊരു ഗ്രഹത്തിന്റെ സാന്നിദ്ധ്യമില്ലാതെ തന്നെ ബുധന്റെ ഓർബിറ്റ് കൃത്യമായി വിശദീകരിക്കാം എന്ന് തെളിഞ്ഞു. അതിന് മറ്റൊരു ഗൗരവകരമായ അർത്ഥം കൂടി ഉണ്ടായിരുന്നു. ന്യൂട്ടന്റെ സിദ്ധാന്തങ്ങളിൽ എവിടെയോ എന്തൊക്കെയോ പോരായ്മകളുണ്ട്!
അതെ, അതുണ്ട്. തത്കാലം അത് തിരിച്ചറിയാനുള്ള എളുപ്പത്തിന് നമുക്കൊരു ചിന്താപരീക്ഷണം നടത്തിനോക്കാം.
ഭൂമി സൂര്യന് ചുറ്റും കറങ്ങുകയാണ്. തത്കാലം മറ്റ് ഗ്രഹങ്ങളുടെ സ്വാധീനം നമുക്ക് അവഗണിക്കാം. ഭൂമിയ്ക്കും സൂര്യനും ഇടയിലുള്ള ഗുരുത്വാകർഷണ ബലമാണ് ഭൂമിയെ ഓർബിറ്റിൽ നിർത്തുന്നത്. ആ ബലം മേൽപ്പറഞ്ഞ സമവാക്യം വഴി കണക്കാക്കാമല്ലോ. അവിടെ M1 സൂര്യന്റെ പിണ്ഡവും M2 ഭൂമിയുടെ പിണ്ഡവും ആണ്. ഇതുവരെ ഓക്കേ ആണല്ലോ അല്ലേ? ഇനി, പെട്ടെന്നൊരു സമയത്ത് സൂര്യൻ അപ്രത്യക്ഷമാകുന്നു എന്ന് സങ്കല്പിക്കുക. അതെങ്ങനെ അപ്രത്യക്ഷമാകും എന്ന് ചോദിക്കരുത്, അപ്രത്യക്ഷമാകുന്നു- അത്രേ ഉള്ളൂ. ചോദ്യം വരുന്നേയുള്ളു. ഭൂമിയുടെ ഓർബിറ്റിന് എന്ത് സംഭവിക്കും? സൂര്യൻ അപ്രത്യക്ഷമായാൽ M1 പൂജ്യമാകും. അപ്പോൾ ഗുരുത്വാകർഷണ ബലവും പൂജ്യമാകും. അപ്പോ ഭൂമിയുടെ മേലുള്ള പിടി ഇല്ലാതാകും. കയറിൽ കെട്ടി കറക്കിക്കൊണ്ടിരുന്ന കല്ല് പിടിവിട്ടാൽ എന്ത് ചെയ്യും? പിടി വിട്ട സ്ഥാനത്ത് വെച്ച് നേർരേഖയിൽ തെറിച്ച് പോകും, അല്ലേ? അപ്പോ ഭൂമിയും അതുപോലെ തെറിയ്ക്കുമോ? വരട്ടെ... പ്രശ്നമുണ്ട്. സൂര്യനിൽ നിന്ന് പ്രകാശം ഭൂമിയിലെത്താൻ എട്ട് മിനിറ്റ് വേണം. അതായത് സൂര്യൻ അപ്രത്യക്ഷമായാലും എട്ട് മിനിറ്റ് കൂടി നമുക്ക് സൂര്യപ്രകാശം ലഭിയ്ക്കും. പക്ഷേ പ്രകാശവേഗതയെ കവച്ചുവെച്ച് ഈ ഭൗതികപ്രപഞ്ചത്തിൽ ഒന്നിനും സഞ്ചരിക്കാനാവില്ല. M1 പൂജ്യമായാലുടൻ ഗുരുത്വബലം (F) പൂജ്യമാകും. പക്ഷേ M1 പൂജ്യമായ കാര്യം ഭൂമിയിൽ അറിയണമെങ്കിൽ 8 മിനിറ്റെങ്കിലും കഴിയണം, കാരണം പ്രകാശത്തെക്കാൾ വേഗത്തിൽ ആ വിവരത്തിന് ഭൂമിയിലെത്താനാവില്ല. അപ്പോൾ, F പൂജ്യമായശേഷവും എട്ട് മിനിറ്റ് കൂടി ഭൂമി ഓർബിറ്റിൽ നിൽക്കേണ്ടി വരും. പക്ഷേ ബലമില്ലാതെ എങ്ങനെ അത് ഓർബിറ്റിൽ നിൽക്കും?
ചോദ്യം മനസിലായോ എന്നുറപ്പിക്കാൻ അവസാനപാരഗ്രാഫ് ഒരിയ്ക്കൽ കൂടി വായിച്ചുനോക്കൂ. ന്യൂട്ടന്റെ നിയമത്തിന്റെ അക്കൗണ്ട് ബുക്കിൽ എവിടേയും എഴുതിച്ചേർക്കാനാകാത്ത ഒരു എട്ട് മിനിറ്റ് ഇവിടെ കിടപ്പുണ്ട്. അത് എവിടെ എഴുതും? സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം വരുന്നതുവരെ ഈ ചോദ്യത്തിന് ഉത്തരമില്ലായിരുന്നു!
ഐൻസ്റ്റൈൻ പറഞ്ഞത്
1915-ലാണ് ഐൻസ്റ്റൈൻ ഗുരുത്വാകർഷണത്തെ കുറിച്ചുള്ള തന്റെ സിദ്ധാന്തം അവതരിപ്പിക്കുന്നത്. ന്യൂട്ടന്റെ സിദ്ധാന്തത്തിലെ കുറവ് പരിഹരിക്കുക എന്നതിനപ്പുറം, അടിസ്ഥാനപരമെന്ന് ശാസ്ത്രലോകം പരക്കെ കരുതിയിരുന്ന ചില ധാരണകളെ ആ സിദ്ധാന്തം അടിച്ചുതകർത്തുകളഞ്ഞു.
തകർത്തുകളഞ്ഞു എന്ന ഭൂതകാലപ്രയോഗം, പക്ഷേ ഭൗതികശാസ്ത്രജ്ഞർക്ക് മാത്രമാണ് ബാധകം. സാധാരണക്കാരെ സംബന്ധിച്ച് ഇപ്പോഴും ആ തകർന്ന ധാരണ തന്നെയാകും മനസിൽ കൊണ്ടുനടക്കുന്നത്. സ്ഥലം (space), കാലം (time) എന്നിവ നമുക്കിപ്പോഴും പരസ്പരം ബന്ധമില്ലാത്ത രണ്ട് അസ്തിത്വങ്ങളാണല്ലോ. ഇരിക്കുന്നിടത്തുനിന്ന് മുറിയുടെ മൂലയിലേക്ക് നോക്കുക, മുറിയുടെ വലിപ്പത്തെക്കുറിച്ച് ആലോചിക്കുക, അകലെ കാണുന്ന നക്ഷത്രം എത്ര ദൂരെയാണെന്ന് ചിന്തിക്കുക, തുടങ്ങിയവയൊക്കെ നമ്മുടെ മസ്തിഷ്കത്തിൽ എത്തിക്കുന്നത് 'സ്ഥലം' എന്ന space-നെ കുറിച്ചുള്ള ഒരു ബോധമാണ് അല്ലേ? മറിച്ച്, നിങ്ങൾ ആ മുറിയിൽ എത്തിയിട്ട് എത്ര നേരമായി എന്നോർക്കുക, മൂലയിലേയ്ക്ക് നടക്കാൻ എത്ര നേരമെടുക്കും എന്നാലോചിക്കുക, തുടങ്ങിയ പ്രവൃത്തികൾ മസ്തിഷ്കത്തിലേയ്ക്ക് എത്തിക്കുന്നത് സമയം എന്ന time-നെ കുറിച്ചുള്ള ബോധമാണ്. ഈ രണ്ട് ബോധങ്ങളും നമ്മെ സംബന്ധിച്ച് തീർത്തും വെവ്വേറെ കാര്യങ്ങളാണ്. 'സമയം ആർക്കുവേണ്ടിയും കാത്തുനിൽക്കുന്നില്ല' എന്ന ഫിലോസഫിക്കൽ ഡയലോഗ് പോലും, സമയത്തെ മറ്റെല്ലാ കാര്യങ്ങളിൽ നിന്നും വേർപെടുത്തി നിർത്തി ചിന്തിക്കാനുള്ള നമ്മുടെ പ്രവണതയുടെ ഫലമാണ്. പക്ഷേ ഐൻസ്റ്റൈൻ ഇവിടെ ചെയ്തത്, സ്ഥലത്തേയും സമയത്തേയും പരസ്പരം കൂട്ടിച്ചേർത്ത് ഒരു പുതിയ അടിസ്ഥാനസങ്കല്പം അങ്ങ് ഉണ്ടാക്കുകയാണ്. ഇതിലൂടെ ഗുരുത്വാകർഷണത്തെ സംബന്ധിച്ച ന്യൂട്ടന്റെ സിദ്ധാന്തങ്ങളുടെ കുറവ് പരിഹരിക്കാനായി. പക്ഷേ മെഴുകുതിരിയുടെ പ്രകാശം കൂട്ടാൻ നടത്തുന്ന ഒരു ഗവേഷണത്തിനും എൽ.ഈ.ഡി. ബൾബിലെത്താനാകില്ലല്ലോ. LED-യുടെ കണ്ടുപിടിത്തം തികച്ചും വേറെ തന്നെ ഒരു വഴിയിലൂടെയാണ് ഉണ്ടാകുന്നത്. അതുപോലെ, ഗുരുത്വാകർഷണത്തെ സംബന്ധിച്ച് കൂടുതൽ മികച്ചതായ ആ സിദ്ധാന്തം ഐൻസ്റ്റൈൻ തീർത്തും വേറെ തന്നെയായ ഒരു വഴിയിലൂടെയാണ് രൂപീകരിച്ചെടുത്തത്.
നാം ജീവിക്കുന്ന ലോകം മൂന്ന് ഡയമെൻഷനുകൾ ഉള്ളതാണെന്ന് പറയാറുണ്ടല്ലോ. മുന്നിലേയ്ക്ക്-പിന്നിലേയ്ക്ക്, മുകളിലേയ്ക്ക്-താഴേയ്ക്ക്, ഇടത്തേയ്ക്ക്-വലത്തേയ്ക്ക് എന്നിങ്ങനെ മൂന്ന് ദിശകളാൽ നമ്മുടെ 'സ്ഥലം' എന്ന ബോധത്തെ നമുക്ക് അടയാളപ്പെടുത്താമെന്നത് എല്ലാവർക്കും അറിയാം. ഐൻസ്റ്റൈൻ ഇതിന് പകരം നാല് ഡയമെൻഷനുകളുള്ള ഒരു പുതിയ ലോകമാതൃക ഉണ്ടാക്കി. മേൽപ്പറഞ്ഞ മൂന്നെണ്ണത്തിനോടൊപ്പം, സമയം എന്ന ബോധത്തെക്കൂടി വിളക്കിച്ചേർക്കുകയാണ് അദ്ദേഹം ചെയ്തത്. ഇത് മനസിൽ ചിത്രീകരിച്ചെടുക്കുക വളരെ പ്രയാസമാണ്. കാരണം, നമ്മുടെ മസ്തിഷ്കം ഈ രണ്ട് ബോധത്തേയും രണ്ട് വ്യത്യസ്ത കാര്യങ്ങളായിട്ടാണ് കൈകാര്യം ചെയ്ത് ശീലിച്ചിരിക്കുന്നത് എന്നത് തന്നെ. പക്ഷേ ഗണിതശാസ്ത്രം കൈകാര്യം ചെയ്യാനറിയുന്നവർക്ക് ഇത് അല്പം കൂടി എളുപ്പമാണ്. മൂന്ന് മാനങ്ങളുള്ള ഒരു സ്പെയ്സിൽ ദൂരങ്ങളേയും സ്ഥാനങ്ങളേയും വിശകലനം ചെയ്യാൻ ഉപയോഗിക്കുന്ന സമവാക്യങ്ങളിലേയ്ക്ക് ഒരു പുതിയ ചരം (variable) കൂടി ചേർത്താലും അവിടെ ഉപയോഗിക്കുന്ന സമവാക്യങ്ങളിൽ ഗണിതപരമായി വലിയ വ്യത്യാസമൊന്നും ഉണ്ടാകില്ല. പക്ഷേ ഗണിതത്തിൽ ഉപയോഗിക്കുന്ന സംഖ്യകൾക്കും ക്രിയകൾക്കും പിന്നിൽ ചില ഭൗതികയാഥാർത്ഥ്യങ്ങൾ ഉണ്ട്. ഉദാഹരണത്തിന്, F = ma എന്ന് പറഞ്ഞാൽ ആ സമവാക്യത്തിലെ F, m, a എന്നീ ചരങ്ങൾ ചില ഭൗതികഗുണങ്ങളേയും അതുകൊണ്ട് തന്നെ അവയെ കൂട്ടിയോജിപ്പിക്കുന്ന സമവാക്യം ഭൗതികലോകത്തിലെ ഒരു സവിശേഷതയേയും സൂചിപ്പിക്കുന്നു. m-ഉം a-യും തമ്മിൽ ഗുണിച്ചാൽ F കിട്ടും എന്നതാണ് അതിന്റെ 'ഗണിതാർത്ഥം'. പക്ഷേ ഒരു പ്രത്യേക അളവിൽ ഒരു വസ്തുവിന്റെ വേഗത കൂട്ടണമെങ്കിൽ, കൂടുതൽ മാസ് (m) ഉള്ള വസ്തുവിന് കൂടുതൽ ബലം (F) കൊടുക്കേണ്ടി വരും, ഒരേ ബലം പല മാസ് ഉള്ള വസ്തുക്കളിൽ പ്രയോഗിച്ചാൽ ഓരോന്നിനും ഉണ്ടാകുന്ന വേഗതവ്യത്യാസം വേറേ വേറെയായിരിക്കും എന്നിങ്ങനെ പല പല ഭൗതികസവിശേഷതകളെയാണ് ആ കൊച്ച് സമവാക്യം സൂചിപ്പിക്കുന്നത്. ഒരു വസ്തുവിന്റെ മാസും, അതിൽ പ്രയോഗിക്കുന്ന ബലവും ഇത്രയിത്രയൊക്കെയാണ് എന്ന് സങ്കല്പിച്ചാൽ അതിന്റെ വേഗത എത്ര വ്യത്യാസപ്പെടും എന്ന് ഈ സമവാക്യത്തിലൂടെ പേപ്പറിൽ കണക്കാക്കിയെടുക്കാം. ഇനി ആ മാസുള്ള ഒരു വസ്തുവിനെ ശരിയ്ക്കും എടുത്ത്, അത്ര തന്നെ ബലം ശരിയ്ക്കും പ്രയോഗിച്ചിട്ട് അതിന്റെ വേഗതയിൽ വരുന്ന മാറ്റം ഒന്ന് അളന്നുനോക്കൂ. പേപ്പറിൽ കിട്ടിയ മൂല്യം തന്നെയാണ് അളക്കുമ്പോഴും കിട്ടുന്നത് എന്ന് കാണാം. ഇങ്ങനെയാണ് ആ സമവാക്യത്തിന്റെ 'ഭൗതികാർത്ഥം' നമ്മൾ പരിശോധിയ്ക്കുന്നത്. പലപ്പോഴും ഗണിതത്തിലെ ഭൗതികാർത്ഥം മനസിലാകാതെ പോകുന്നത് കൊണ്ടാണ് നമ്മളിൽ ഭൂരിഭാഗം പേർക്കും ഗണിതം ഒരു പേടിസ്വപ്നമായി മാറുന്നത്. അതെന്തായാലും, ഗണിതഭാഷയിലാണ് ആധുനിക ഭൗതികശാസ്ത്രം സംസാരിക്കുന്നത്. F = ma പോലുള്ള ലളിതസമവാക്യങ്ങളാകില്ല എപ്പോഴും എന്നേയുള്ളു. ഉദാഹരണത്തിന് താഴെ കാണുന്ന സമവാക്യം ആട്ടിവിട്ട ഒരു ഊഞ്ഞാലിന്റെ ചലനത്തെ വിശദീകരിക്കുന്നതാണ്.
ഇത് ഗണിതം പഠിയ്ക്കാത്ത ഒരാൾക്ക് മനസിലാകുന്ന ഒന്നല്ല. സാധാരണ സ്കൂൾ ഗണിതത്തിൽ ഉൾപ്പെടുത്താനാവാത്ത വിധം സങ്കീർണമായ ഒരുപാട് ഗണിതോപകരണങ്ങൾ (mathematical tools) ഇതിൽ ഉപയോഗിച്ചിരിക്കുന്നു. ഇത്ര തന്നെയോ ഇതിലും എത്രയോ മടങ്ങോ പോലും സങ്കീർണമായ ഗണിതമാണ് ഇന്നത്തെ ആധുനിക ഭൗതികശാസ്ത്രം ഉപയോഗിക്കുന്നത്. പക്ഷേ സമവാക്യം എത്ര തന്നെ സങ്കീർണമായാലും F = ma യ്ക്ക് ഉള്ളതുപോലെ ഗണിതാർത്ഥത്തിന് പുറമേ ഒരു ഭൗതികാർത്ഥം കൂടി അവയ്ക്കുണ്ടാകും. ക്വാണ്ടം സിദ്ധാന്തം, ആപേക്ഷികത തുടങ്ങിയ വിഷയങ്ങൾ സാധാരണക്കാരോട് പറഞ്ഞുകൊടുക്കുമ്പോൾ വരുന്ന വെല്ലുവിളി, സമവാക്യങ്ങൾ ഇല്ലാതെ അവയുടെ ഭൗതികാർത്ഥം മാത്രം അവതരിപ്പിക്കുക എന്നതാണ്. നമ്മുടെ സാമാന്യബുദ്ധിയിലെ തോന്നലുകൾക്ക് ശരിയെന്ന് തോന്നാത്ത വിചിത്രമായ ഭൗതികാർത്ഥങ്ങളാണ് ആപേക്ഷികതയിലെ സമവാക്യങ്ങൾക്ക്. "അതെങ്ങനെ?" എന്നൊരു മറുചോദ്യം ഉറപ്പായും വരും. അതിന് സാധ്യമായ മറുപടി സമവാക്യങ്ങൾ കാണിച്ചുകൊടുക്കുക എന്നതേ ഉള്ളൂ. പക്ഷേ ഉയർന്ന ഗണിതം അറിയാത്തവർക്ക് ആ സമവാക്യങ്ങളെ ഗ്രഹിക്കാനാകില്ല. അതോടെ അവിടം dead-end ആകുന്നു. പക്ഷേ അവ സാമാന്യബുദ്ധിയ്ക്ക് നിരക്കുന്നില്ല എന്നതിന് അവ തെറ്റാണ് എന്നല്ല അർത്ഥം. F = ma യെ ഒരു വസ്തുവിൽ ബലം പ്രയോഗിച്ച് അതിന്റെ വേഗതവ്യത്യാസം അളന്ന് ബോധ്യപ്പെടാവുന്നത് പോലെ, ഈ സമവാക്യങ്ങളെയും നമുക്ക് പരീക്ഷിച്ച് ബോധ്യപ്പെടാം. ഇന്നയിന്ന സാഹചര്യങ്ങളിൽ ഇന്നയിന്നപോലെ കാര്യങ്ങൾ നടക്കും എന്ന് ഒരു സമവാക്യം സൂചിപ്പിച്ചാൽ അതിനെ ഒരു സൈദ്ധാന്തിക പ്രവചനം ആയിട്ട് കണക്കാക്കാം. നെപ്റ്റ്യൂൺ ഗ്രഹത്തിനെ ന്യൂട്ടന്റെ സമവാക്യങ്ങൾ സൈദ്ധാന്തികമായി പ്രവചിച്ചത് നമ്മൾ കണ്ടല്ലോ. അതുപോലെ സൈദ്ധാന്തിക പ്രവചനങ്ങൾ സത്യമാകുന്നുണ്ടോ എന്ന് ഉചിതമായ സാഹചര്യങ്ങളിൽ നിരീക്ഷണമോ പരീക്ഷണമോ വഴി പരിശോധിക്കാവുന്നതേയുള്ളു. ആവർത്തിച്ചുള്ള പരിശോധനകൾ പ്രവചനങ്ങളെ ശരിവെക്കുന്നു എങ്കിൽ അതാ സിദ്ധാന്തം ശരിയായിരിക്കും എന്നാണ് സൂചിപ്പിക്കുന്നത്. സാമാന്യബുദ്ധിയെ കൊഞ്ഞനം കുത്തിയിട്ടും ആപേക്ഷികതയും ക്വാണ്ടം ഫിസിക്സുമൊക്കെ ഇന്ന് നമ്മുടെ അടിസ്ഥാനധാരണകളായി നിലനിൽക്കുന്നത് അവയെ നാം പല തവണ പരീക്ഷിച്ച് ബോധ്യപ്പെട്ടതുകൊണ്ടാണ്. ഐൻസ്റ്റൈന്റെ ആപേക്ഷികതാ സിദ്ധാന്തങ്ങളുടെ മിക്ക പ്രവചനങ്ങളും നാം പരീക്ഷിച്ച് ബോധ്യപ്പെട്ടിട്ടുണ്ട്. എന്നാൽ ചില കാര്യങ്ങൾ നമുക്ക് 'പരീക്ഷിക്കാൻ' സാധിക്കില്ല. ഒരു സൈദ്ധാന്തിക പ്രവചനം സത്യമാണോ എന്ന് തെളിയിക്കാൻ കൃത്രിമമായി സാഹചര്യങ്ങൾ സൃഷ്ടിക്കുകയാണ് പരീക്ഷണത്തിൽ ചെയ്യുന്നത്. ഹിഗ്സ് ബോസോണിന്റെ കണ്ടെത്തലിന് കണികാപരീക്ഷണ ശാല എന്ന കൃത്രിമ സംവിധാനം ഉണ്ടാക്കിയത് ഒരു ഉദാഹരണമാണ്. പക്ഷേ ഗുരുത്വതരംഗങ്ങളെക്കുറിച്ച് ആപേക്ഷികത പറയുന്നത് അതിഭീമൻ പിണ്ഡമുള്ള വസ്തുക്കളുടെ ചലനവുമായി ബന്ധപ്പെട്ടാണ്. ഒരു നക്ഷത്രം എടുത്ത് ചുഴറ്റുന്നതോ ബ്ലാക്ഹോളിനെ എടുത്ത് കുലുക്കുന്നതോ ഒന്നും കൃത്രിമമായി സൃഷ്ടിക്കുക സാധ്യമല്ലല്ലോ. അവിടെ പരീക്ഷണം അല്ല, മറിച്ച് നിരീക്ഷണം മാത്രമേ സാധിയ്ക്കൂ. അതിന് മതിയായ സാഹചര്യങ്ങൾ പ്രപഞ്ചത്തിൽ സ്വാഭാവികമായി ഉണ്ടാകുന്നത് വരെ കാത്തിരിക്കേണ്ടിവരും. ഗുരുത്വതരംഗങ്ങളെ കാണാൻ, അവയെക്കുറിച്ചുള്ള സൈദ്ധാന്തിക പ്രവചനം നടന്നശേഷം നൂറ് വർഷങ്ങൾ കാത്തിരിക്കേണ്ടിവന്നു!
ഇനിയും ഞാൻ കാര്യത്തിലേയ്ക്ക് കടന്നില്ലല്ലോ എന്ന പരാതി കാണും. സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം എന്ന, കേൾക്കുമ്പോൾ അതിവിചിത്രമായ സിദ്ധാന്തത്തിലേയ്ക്ക് പെട്ടെന്ന് എടുത്ത് ചാടിയിട്ട് കാര്യമില്ല. അതിന് ചില മുന്നൊരുക്കങ്ങൾ കൂടിയേ തീരൂ. അതിനാണ് നാമിവിടെ ശ്രമിക്കുന്നത്. സാമാന്യ ആപേക്ഷികതയിലേയ്ക്ക് ഐൻസ്റ്റൈൻ എത്തിച്ചേരുന്നത് സമാനതാ സിദ്ധാന്തം (principle of equivalence) എന്ന മറ്റൊരു സിദ്ധാന്തത്തിൽ നിന്നാണ്.
നിങ്ങൾ ഒരു ലിഫ്റ്റിലാണ്. പതിനെട്ടാം നിലയിൽ നിന്നും താഴേയ്ക്കുള്ള വരവിനിടെ ഭാഗ്യം കൊണ്ട് ഈ ലിഫ്റ്റിന്റെ കെട്ട് പൊട്ടി എന്ന് സങ്കല്പിക്കുക. ചാവാൻ പോകുമ്പോഴും ഫിസിക്സ് പഠിയ്ക്കാനുള്ള താത്പര്യം ഉള്ള വിചിത്രജീവിയാണ് നിങ്ങൾ എന്നുകൂടി സങ്കല്പിച്ചുകൊണ്ട് ചോദിക്കട്ടെ, താഴേയ്ക്ക് വീഴുമ്പോൾ നിങ്ങൾക്ക് എന്താകും അനുഭവപ്പെടുക? ഒരു സ്പ്രിങ് ബാലൻസിൽ കല്ല് കെട്ടിത്തൂക്കിയിട്ട് അത് താഴേയ്ക്ക് വിട്ടാൽ വീഴുന്ന സമയത്ത് കല്ലിന്റെ ഭാരം പൂജ്യം കാണിക്കും. അതുപോലെ താഴേയ്ക്ക് വീഴുന്ന ആളിനും ഭാരമില്ലായ്മ അനുഭവപ്പെടും. അതായത് സ്വതന്ത്രമായി താഴേയ്ക്കുവീഴുക എന്ന ഫ്രീഫോൾ (free-fall) അവസ്ഥയിൽ ഗുരുത്വാകർഷണം നിങ്ങൾക്ക് അനുഭവപ്പെടില്ല. ഇതിനെ മറ്റൊരു രീതിയിൽ കൂടി ആലോചിക്കാം. നിങ്ങൾ ഒരു സ്പെയ്സ് ഷിപ്പിലാണ്. ബാഹ്യകാശത്തുകൂടി അത് സ്വതന്ത്രമായി നീങ്ങിക്കൊണ്ടിരിക്കുന്നു. ഷിപ്പിന്റെ എഞ്ചിൻ ഓഫാണ്. നിങ്ങൾ തീർത്തും ഭാരരഹിതമായി അതിനുള്ളിൽ പൊങ്ങിക്കിടക്കുന്നു. പെട്ടെന്ന് നിങ്ങൾ അതിന്റെ ഒരു ചുവരിലേയ്ക്ക് വലിയ്ക്കപ്പെടുന്നു. ഒന്നുകിൽ നിങ്ങളുടെ സ്പെയ്സ് ഷിപ്പിന്റെ എഞ്ചിൻ ഓണായി അത് accelerate ചെയ്യപ്പെട്ടതാണ് (നിർത്തിയിട്ടിരിക്കുന്ന ബസ് മുന്നോട്ടെടുക്കുമ്പോൾ സീറ്റിലേയ്ക്ക് അമർത്തപ്പെടുന്നതുപോലെ) അല്ലെങ്കിൽ നിങ്ങളുടെ സ്പെയ്സ് ഷിപ്പ് ഏതോ ആകാശഗോളത്തിന്റെ ഗ്രാവിറ്റിയുടെ പരിധിയിലേയ്ക്ക് കടന്നിരിക്കുന്നു. ആ ഗോളം നിങ്ങളിൽ ഗുരുത്വാകർഷണം ചെലുത്തുകയാണ്. ഇതിൽ ഏതാണ് സംഭവിച്ചിരിക്കുന്നത് എന്നറിയാൻ മാർഗമുണ്ടോ? ഇല്ല. സ്പെയ്സ് ഷിപ്പിനുള്ളിലിരുന്നുകൊണ്ട് പുറംലോകവുമായി ഏതെങ്കിലും രീതിയിൽ ബന്ധപ്പെടാതെ, അത് accelerate ചെയ്തതാണോ ഏതെങ്കിലും ഗുരുത്വാകർഷണ ബലത്തിന് വിധേയമായതാണോ എന്ന് കണ്ടെത്താൻ നിങ്ങൾക്ക് സാധിക്കില്ല. ഒരു പരീക്ഷണത്തിനും ഈ രണ്ട് പ്രഭാവങ്ങളേയും തമ്മിൽ വേർതിരിച്ചറിയാൻ പറ്റില്ല. ഇതാണ് സാമാനതാ സിദ്ധാന്തം.
അതായത്, ഒരു വസ്തുവിന് acceleration അഥവാ ത്വരണം സംഭവിക്കുന്നതും അതിൽ ഒരു ഗുരുത്വാകർഷബലം ചെലുത്തപ്പെടുന്നതും തമ്മിൽ യാതൊരു വ്യത്യാസവും ഇല്ല. അങ്ങനെയെങ്കിൽ ആപ്പിൾ താഴേയ്ക്ക് ത്വരണത്തിന് വിധേയമാകുന്നതാണ്, ഭൂമി അതിനെ ആകർഷിക്കുകയൊന്നും ചെയ്യുന്നില്ല എന്നാണെങ്കിലോ? ഗുരുത്വാകർഷണബലം പ്രയോഗിക്കാതെ തന്നെ, വേറെ ഏതെങ്കിലും കാരണം കൊണ്ടാണ് ആപ്പിൾ ത്വരണത്തിന് വിധേയമാകുന്നത് എങ്കിലോ? അപ്പോ, ഗുരുത്വാകർഷണ ബലം എന്നൊരു ബലമേ ഇല്ലെങ്കിലോ?
വളഞ്ഞ സ്ഥലകാലം
ഒരു വസ്തുവിന്റെ സ്ഥാനമോ ചലനമോ പറയുന്നതിനും പഠിക്കുന്നതിനും അതിനെ ഏതെങ്കിലും ഒരു റഫറൻസുമായി താരതമ്യം ചെയ്യേണ്ടതുണ്ട്. ഉദാഹരണത്തിന്, ഒരു പേപ്പറിൽ ഒരു മുത്ത് ഇരിക്കുന്നു. അതിന്റെ പേപ്പറിലെ സ്ഥാനം പറയാൻ, പേപ്പറിന്റെ ഒരു മൂലയെ കേന്ദ്രബിന്ദുവും അവിടന്ന് പരസ്പരം ലംബമായ രണ്ട് വക്കുകളെ അക്ഷങ്ങളായും എടുത്ത് ഒരു നിർദേശാങ്ക സംവിധാനം സങ്കല്പിക്കാം. ഇതിൽ ഇടത്തുനിന്ന് വലത്തേയ്ക്കുള്ള ദിശയെ x-ദിശ എന്നും താഴെ നിന്ന് മുകളിലേയ്ക്കുള്ള ദിശയെ y-ദിശ എന്നും വിളിക്കാം. ഇനി ആ മുത്തിന്റെ സ്ഥാനം പറയാൻ രണ്ട് ദൂരങ്ങൾ പറഞ്ഞാൽ മതി. ഈ രണ്ട് ദിശകളിലും ഈ മുത്ത്, കേന്ദ്രബിന്ദുവിൽ നിന്ന് എത്ര ദൂരെയാണ് എന്നാണ് അവ സൂചിപ്പിക്കുന്നത്. ഈ രണ്ട് അക്ഷങ്ങളുടെ ദിശയിലുള്ള ഏത് രണ്ട് ദൂരങ്ങൾ പറഞ്ഞാലും അത് ഏതെങ്കിലുമൊരു പ്രത്യേക ബിന്ദുവിന്റെ സ്ഥാനത്തെ സൂചിപ്പിക്കും. അവയെ ക്രമത്തിൽ (x,y) എന്നിങ്ങനെ എഴുതുകയാണ് പതിവ്. അതായത് ഓരോ ജോഡി (x,y)-യും ഒരു പ്രത്യേക സ്ഥാനമാണ്. അവയെ നിർദേശാങ്കങ്ങൾ (coordinates) എന്ന് വിളിക്കുന്നു. ഇപ്പോൾ പേപ്പർ പ്രതലത്തിലെ മുത്തിന്റെ സ്ഥാനം ഒരു ജോഡി സംഖ്യകൾ എന്ന ഗണിതരൂപം കൈവരിച്ചിരിക്കുന്നതായി കാണാം.
ഇനി ഒരു ഗണിതക്രിയയിൽ ഇതിലെ x-ഉം y-യും മാറുന്നു എങ്കിൽ അതിന്റെ അർത്ഥം എന്താണ്? x-ഉം y-യും സ്ഥാനത്തെ സൂചിപ്പിക്കുന്നു, അവ മാറിയാൽ സ്ഥാനം മാറുന്നു, സ്ഥാനം മാറുക എന്നാൽ അത് ചലനത്തെ സൂചിപ്പിക്കുന്നു. ഇങ്ങനെ നിർദേശാങ്കങ്ങളിലെ മാറ്റമായിട്ട് ചലനത്തെ നമുക്ക് വിശദീകരിക്കാനാകുന്നു. സ്ഥാനത്തേയും ചലനത്തേയും ഭൗതികശാസ്ത്രം കൈകാര്യം ചെയ്യുന്നത് ഇങ്ങനെയാണ്. പേപ്പറിന് പകരം ഒരു മുറിയിലെ ഈച്ചയുടെ ചലനമാണ് സൂചിപ്പിക്കേണ്ടത് എങ്കിൽ മുറിയുടെ ഒരു മൂലയെ കേന്ദ്രബിന്ദുവാക്കി, പരസ്പരം ലംബമായ മൂന്ന് അക്ഷങ്ങൾ സങ്കല്പിക്കാനാകും. പേപ്പർ എന്ന 2D വസ്തുവിന് രണ്ട് നിർദേശാങ്കങ്ങൾ മതിയായിരുന്നു. മുറി 3D ആയതിനാൽ നിർദേശാങ്കങ്ങളും മൂന്ന് വേണ്ടിവരും എന്നേയുള്ളു.
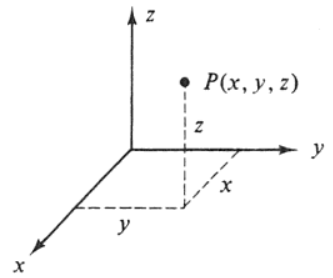
ഒരു 3D സ്പെയ്സിൽ മൂന്ന് സ്ഥാന നിർദേശാങ്കങ്ങളെയും സമയത്തേയും ബന്ധിപ്പിച്ച്, സമയം മാറുമ്പോൾ നിർദേശാങ്കങ്ങൾ എങ്ങനെ മാറുന്നു എന്ന് സൂചിപ്പിക്കുന്ന ഒരു ഗണിതസമവാക്യം ഉണ്ടെങ്കിൽ അത് ഒരു വസ്തുവിന്റെ ചലനത്തെ ഗണിതരൂപത്തിൽ ഒരു പേപ്പറിൽ വിശദീകരിക്കാനാകും.
നിർദേശാങ്കങ്ങൾ എന്ന സങ്കല്പത്തെ പരിചയപ്പെടുത്താനാണ് ഇത്രയും പറഞ്ഞത്. ഇപ്പോൾ കണ്ട, പരസ്പരം ലംബമായ അക്ഷങ്ങളെ ഉപയോഗിക്കുന്ന നിർദേശാങ്കരീതിയെ കാർട്ടേസ്യൻ രീതി (Cartesian system) എന്നാണ് വിളിക്കുന്നത്. എന്നാൽ എല്ലായ്പ്പോഴും ഈ രീതി തന്നെ തുടരണം എന്നില്ല. ഒരു വസ്തുവിന്റെ സ്ഥാനത്തെ കുറച്ച് സംഖ്യകളുടെ രൂപത്തിൽ സൂചിപ്പിക്കാനാകുന്ന ഏത് സമ്പ്രദായവും ഉപയോഗിക്കാം. സാഹചര്യത്തിന് ഏറ്റവും സൗകര്യപ്രദമായത് നമ്മൾ തെരെഞ്ഞെടുക്കും. ഉദാഹരണത്തിന് നമുക്കൊക്കെ ഏറേ പരിചിതമായ ഒരു നിർദേശാങ്ക സമ്പ്രദായമാണ് അക്ഷാംശവും രേഖാംശവും (latitude-longitude).
ഭൂമിയുടെ ഉപരിതലത്തിൽ സ്ഥാനവും ചലനവും പറയാൻ റഫറൻസായി നാമത് ഉപയോഗിക്കുന്നു. ഇത് പക്ഷേ കാർട്ടേസ്യൻ രീതിയല്ല പിൻതുടരുന്നത്. എന്താണ് പ്രശ്നം? കാർട്ടേസ്യൻ രീതിയിൽ പരസ്പരം ലംബമായ നേർദിശകളാണ് നമ്മൾ ഉപയോഗിച്ചത്. ഭൂമിയുടെ ഉപരിതലത്തിൽ ഇത് സാധ്യമാണോ? രേഖാശരേഖകൾ മധ്യരേഖാ പ്രദേശങ്ങളിൽ സമാന്തരമാണെങ്കിലും ഭൂമിയുടെ ഗോളാകൃതി കാരണം അവ ധ്രുവപ്രദേശങ്ങളിൽ വച്ച് കൂടിച്ചേരുന്നു. ഈ ഭൂമിയുടെ ഉപരിതലത്തിൽ ഒരു വലിയ ത്രികോണം വരച്ചിട്ട് അതിന്റെ മൂന്ന് കോണുകൾ അളന്ന് കൂട്ടിയാൽ 180 ഡിഗ്രി ആയിരിക്കില്ല, കൂടുതലുണ്ടാകും!
തകർത്തുകളഞ്ഞു എന്ന ഭൂതകാലപ്രയോഗം, പക്ഷേ ഭൗതികശാസ്ത്രജ്ഞർക്ക് മാത്രമാണ് ബാധകം. സാധാരണക്കാരെ സംബന്ധിച്ച് ഇപ്പോഴും ആ തകർന്ന ധാരണ തന്നെയാകും മനസിൽ കൊണ്ടുനടക്കുന്നത്. സ്ഥലം (space), കാലം (time) എന്നിവ നമുക്കിപ്പോഴും പരസ്പരം ബന്ധമില്ലാത്ത രണ്ട് അസ്തിത്വങ്ങളാണല്ലോ. ഇരിക്കുന്നിടത്തുനിന്ന് മുറിയുടെ മൂലയിലേക്ക് നോക്കുക, മുറിയുടെ വലിപ്പത്തെക്കുറിച്ച് ആലോചിക്കുക, അകലെ കാണുന്ന നക്ഷത്രം എത്ര ദൂരെയാണെന്ന് ചിന്തിക്കുക, തുടങ്ങിയവയൊക്കെ നമ്മുടെ മസ്തിഷ്കത്തിൽ എത്തിക്കുന്നത് 'സ്ഥലം' എന്ന space-നെ കുറിച്ചുള്ള ഒരു ബോധമാണ് അല്ലേ? മറിച്ച്, നിങ്ങൾ ആ മുറിയിൽ എത്തിയിട്ട് എത്ര നേരമായി എന്നോർക്കുക, മൂലയിലേയ്ക്ക് നടക്കാൻ എത്ര നേരമെടുക്കും എന്നാലോചിക്കുക, തുടങ്ങിയ പ്രവൃത്തികൾ മസ്തിഷ്കത്തിലേയ്ക്ക് എത്തിക്കുന്നത് സമയം എന്ന time-നെ കുറിച്ചുള്ള ബോധമാണ്. ഈ രണ്ട് ബോധങ്ങളും നമ്മെ സംബന്ധിച്ച് തീർത്തും വെവ്വേറെ കാര്യങ്ങളാണ്. 'സമയം ആർക്കുവേണ്ടിയും കാത്തുനിൽക്കുന്നില്ല' എന്ന ഫിലോസഫിക്കൽ ഡയലോഗ് പോലും, സമയത്തെ മറ്റെല്ലാ കാര്യങ്ങളിൽ നിന്നും വേർപെടുത്തി നിർത്തി ചിന്തിക്കാനുള്ള നമ്മുടെ പ്രവണതയുടെ ഫലമാണ്. പക്ഷേ ഐൻസ്റ്റൈൻ ഇവിടെ ചെയ്തത്, സ്ഥലത്തേയും സമയത്തേയും പരസ്പരം കൂട്ടിച്ചേർത്ത് ഒരു പുതിയ അടിസ്ഥാനസങ്കല്പം അങ്ങ് ഉണ്ടാക്കുകയാണ്. ഇതിലൂടെ ഗുരുത്വാകർഷണത്തെ സംബന്ധിച്ച ന്യൂട്ടന്റെ സിദ്ധാന്തങ്ങളുടെ കുറവ് പരിഹരിക്കാനായി. പക്ഷേ മെഴുകുതിരിയുടെ പ്രകാശം കൂട്ടാൻ നടത്തുന്ന ഒരു ഗവേഷണത്തിനും എൽ.ഈ.ഡി. ബൾബിലെത്താനാകില്ലല്ലോ. LED-യുടെ കണ്ടുപിടിത്തം തികച്ചും വേറെ തന്നെ ഒരു വഴിയിലൂടെയാണ് ഉണ്ടാകുന്നത്. അതുപോലെ, ഗുരുത്വാകർഷണത്തെ സംബന്ധിച്ച് കൂടുതൽ മികച്ചതായ ആ സിദ്ധാന്തം ഐൻസ്റ്റൈൻ തീർത്തും വേറെ തന്നെയായ ഒരു വഴിയിലൂടെയാണ് രൂപീകരിച്ചെടുത്തത്.
നാം ജീവിക്കുന്ന ലോകം മൂന്ന് ഡയമെൻഷനുകൾ ഉള്ളതാണെന്ന് പറയാറുണ്ടല്ലോ. മുന്നിലേയ്ക്ക്-പിന്നിലേയ്ക്ക്, മുകളിലേയ്ക്ക്-താഴേയ്ക്ക്, ഇടത്തേയ്ക്ക്-വലത്തേയ്ക്ക് എന്നിങ്ങനെ മൂന്ന് ദിശകളാൽ നമ്മുടെ 'സ്ഥലം' എന്ന ബോധത്തെ നമുക്ക് അടയാളപ്പെടുത്താമെന്നത് എല്ലാവർക്കും അറിയാം. ഐൻസ്റ്റൈൻ ഇതിന് പകരം നാല് ഡയമെൻഷനുകളുള്ള ഒരു പുതിയ ലോകമാതൃക ഉണ്ടാക്കി. മേൽപ്പറഞ്ഞ മൂന്നെണ്ണത്തിനോടൊപ്പം, സമയം എന്ന ബോധത്തെക്കൂടി വിളക്കിച്ചേർക്കുകയാണ് അദ്ദേഹം ചെയ്തത്. ഇത് മനസിൽ ചിത്രീകരിച്ചെടുക്കുക വളരെ പ്രയാസമാണ്. കാരണം, നമ്മുടെ മസ്തിഷ്കം ഈ രണ്ട് ബോധത്തേയും രണ്ട് വ്യത്യസ്ത കാര്യങ്ങളായിട്ടാണ് കൈകാര്യം ചെയ്ത് ശീലിച്ചിരിക്കുന്നത് എന്നത് തന്നെ. പക്ഷേ ഗണിതശാസ്ത്രം കൈകാര്യം ചെയ്യാനറിയുന്നവർക്ക് ഇത് അല്പം കൂടി എളുപ്പമാണ്. മൂന്ന് മാനങ്ങളുള്ള ഒരു സ്പെയ്സിൽ ദൂരങ്ങളേയും സ്ഥാനങ്ങളേയും വിശകലനം ചെയ്യാൻ ഉപയോഗിക്കുന്ന സമവാക്യങ്ങളിലേയ്ക്ക് ഒരു പുതിയ ചരം (variable) കൂടി ചേർത്താലും അവിടെ ഉപയോഗിക്കുന്ന സമവാക്യങ്ങളിൽ ഗണിതപരമായി വലിയ വ്യത്യാസമൊന്നും ഉണ്ടാകില്ല. പക്ഷേ ഗണിതത്തിൽ ഉപയോഗിക്കുന്ന സംഖ്യകൾക്കും ക്രിയകൾക്കും പിന്നിൽ ചില ഭൗതികയാഥാർത്ഥ്യങ്ങൾ ഉണ്ട്. ഉദാഹരണത്തിന്, F = ma എന്ന് പറഞ്ഞാൽ ആ സമവാക്യത്തിലെ F, m, a എന്നീ ചരങ്ങൾ ചില ഭൗതികഗുണങ്ങളേയും അതുകൊണ്ട് തന്നെ അവയെ കൂട്ടിയോജിപ്പിക്കുന്ന സമവാക്യം ഭൗതികലോകത്തിലെ ഒരു സവിശേഷതയേയും സൂചിപ്പിക്കുന്നു. m-ഉം a-യും തമ്മിൽ ഗുണിച്ചാൽ F കിട്ടും എന്നതാണ് അതിന്റെ 'ഗണിതാർത്ഥം'. പക്ഷേ ഒരു പ്രത്യേക അളവിൽ ഒരു വസ്തുവിന്റെ വേഗത കൂട്ടണമെങ്കിൽ, കൂടുതൽ മാസ് (m) ഉള്ള വസ്തുവിന് കൂടുതൽ ബലം (F) കൊടുക്കേണ്ടി വരും, ഒരേ ബലം പല മാസ് ഉള്ള വസ്തുക്കളിൽ പ്രയോഗിച്ചാൽ ഓരോന്നിനും ഉണ്ടാകുന്ന വേഗതവ്യത്യാസം വേറേ വേറെയായിരിക്കും എന്നിങ്ങനെ പല പല ഭൗതികസവിശേഷതകളെയാണ് ആ കൊച്ച് സമവാക്യം സൂചിപ്പിക്കുന്നത്. ഒരു വസ്തുവിന്റെ മാസും, അതിൽ പ്രയോഗിക്കുന്ന ബലവും ഇത്രയിത്രയൊക്കെയാണ് എന്ന് സങ്കല്പിച്ചാൽ അതിന്റെ വേഗത എത്ര വ്യത്യാസപ്പെടും എന്ന് ഈ സമവാക്യത്തിലൂടെ പേപ്പറിൽ കണക്കാക്കിയെടുക്കാം. ഇനി ആ മാസുള്ള ഒരു വസ്തുവിനെ ശരിയ്ക്കും എടുത്ത്, അത്ര തന്നെ ബലം ശരിയ്ക്കും പ്രയോഗിച്ചിട്ട് അതിന്റെ വേഗതയിൽ വരുന്ന മാറ്റം ഒന്ന് അളന്നുനോക്കൂ. പേപ്പറിൽ കിട്ടിയ മൂല്യം തന്നെയാണ് അളക്കുമ്പോഴും കിട്ടുന്നത് എന്ന് കാണാം. ഇങ്ങനെയാണ് ആ സമവാക്യത്തിന്റെ 'ഭൗതികാർത്ഥം' നമ്മൾ പരിശോധിയ്ക്കുന്നത്. പലപ്പോഴും ഗണിതത്തിലെ ഭൗതികാർത്ഥം മനസിലാകാതെ പോകുന്നത് കൊണ്ടാണ് നമ്മളിൽ ഭൂരിഭാഗം പേർക്കും ഗണിതം ഒരു പേടിസ്വപ്നമായി മാറുന്നത്. അതെന്തായാലും, ഗണിതഭാഷയിലാണ് ആധുനിക ഭൗതികശാസ്ത്രം സംസാരിക്കുന്നത്. F = ma പോലുള്ള ലളിതസമവാക്യങ്ങളാകില്ല എപ്പോഴും എന്നേയുള്ളു. ഉദാഹരണത്തിന് താഴെ കാണുന്ന സമവാക്യം ആട്ടിവിട്ട ഒരു ഊഞ്ഞാലിന്റെ ചലനത്തെ വിശദീകരിക്കുന്നതാണ്.
ഇത് ഗണിതം പഠിയ്ക്കാത്ത ഒരാൾക്ക് മനസിലാകുന്ന ഒന്നല്ല. സാധാരണ സ്കൂൾ ഗണിതത്തിൽ ഉൾപ്പെടുത്താനാവാത്ത വിധം സങ്കീർണമായ ഒരുപാട് ഗണിതോപകരണങ്ങൾ (mathematical tools) ഇതിൽ ഉപയോഗിച്ചിരിക്കുന്നു. ഇത്ര തന്നെയോ ഇതിലും എത്രയോ മടങ്ങോ പോലും സങ്കീർണമായ ഗണിതമാണ് ഇന്നത്തെ ആധുനിക ഭൗതികശാസ്ത്രം ഉപയോഗിക്കുന്നത്. പക്ഷേ സമവാക്യം എത്ര തന്നെ സങ്കീർണമായാലും F = ma യ്ക്ക് ഉള്ളതുപോലെ ഗണിതാർത്ഥത്തിന് പുറമേ ഒരു ഭൗതികാർത്ഥം കൂടി അവയ്ക്കുണ്ടാകും. ക്വാണ്ടം സിദ്ധാന്തം, ആപേക്ഷികത തുടങ്ങിയ വിഷയങ്ങൾ സാധാരണക്കാരോട് പറഞ്ഞുകൊടുക്കുമ്പോൾ വരുന്ന വെല്ലുവിളി, സമവാക്യങ്ങൾ ഇല്ലാതെ അവയുടെ ഭൗതികാർത്ഥം മാത്രം അവതരിപ്പിക്കുക എന്നതാണ്. നമ്മുടെ സാമാന്യബുദ്ധിയിലെ തോന്നലുകൾക്ക് ശരിയെന്ന് തോന്നാത്ത വിചിത്രമായ ഭൗതികാർത്ഥങ്ങളാണ് ആപേക്ഷികതയിലെ സമവാക്യങ്ങൾക്ക്. "അതെങ്ങനെ?" എന്നൊരു മറുചോദ്യം ഉറപ്പായും വരും. അതിന് സാധ്യമായ മറുപടി സമവാക്യങ്ങൾ കാണിച്ചുകൊടുക്കുക എന്നതേ ഉള്ളൂ. പക്ഷേ ഉയർന്ന ഗണിതം അറിയാത്തവർക്ക് ആ സമവാക്യങ്ങളെ ഗ്രഹിക്കാനാകില്ല. അതോടെ അവിടം dead-end ആകുന്നു. പക്ഷേ അവ സാമാന്യബുദ്ധിയ്ക്ക് നിരക്കുന്നില്ല എന്നതിന് അവ തെറ്റാണ് എന്നല്ല അർത്ഥം. F = ma യെ ഒരു വസ്തുവിൽ ബലം പ്രയോഗിച്ച് അതിന്റെ വേഗതവ്യത്യാസം അളന്ന് ബോധ്യപ്പെടാവുന്നത് പോലെ, ഈ സമവാക്യങ്ങളെയും നമുക്ക് പരീക്ഷിച്ച് ബോധ്യപ്പെടാം. ഇന്നയിന്ന സാഹചര്യങ്ങളിൽ ഇന്നയിന്നപോലെ കാര്യങ്ങൾ നടക്കും എന്ന് ഒരു സമവാക്യം സൂചിപ്പിച്ചാൽ അതിനെ ഒരു സൈദ്ധാന്തിക പ്രവചനം ആയിട്ട് കണക്കാക്കാം. നെപ്റ്റ്യൂൺ ഗ്രഹത്തിനെ ന്യൂട്ടന്റെ സമവാക്യങ്ങൾ സൈദ്ധാന്തികമായി പ്രവചിച്ചത് നമ്മൾ കണ്ടല്ലോ. അതുപോലെ സൈദ്ധാന്തിക പ്രവചനങ്ങൾ സത്യമാകുന്നുണ്ടോ എന്ന് ഉചിതമായ സാഹചര്യങ്ങളിൽ നിരീക്ഷണമോ പരീക്ഷണമോ വഴി പരിശോധിക്കാവുന്നതേയുള്ളു. ആവർത്തിച്ചുള്ള പരിശോധനകൾ പ്രവചനങ്ങളെ ശരിവെക്കുന്നു എങ്കിൽ അതാ സിദ്ധാന്തം ശരിയായിരിക്കും എന്നാണ് സൂചിപ്പിക്കുന്നത്. സാമാന്യബുദ്ധിയെ കൊഞ്ഞനം കുത്തിയിട്ടും ആപേക്ഷികതയും ക്വാണ്ടം ഫിസിക്സുമൊക്കെ ഇന്ന് നമ്മുടെ അടിസ്ഥാനധാരണകളായി നിലനിൽക്കുന്നത് അവയെ നാം പല തവണ പരീക്ഷിച്ച് ബോധ്യപ്പെട്ടതുകൊണ്ടാണ്. ഐൻസ്റ്റൈന്റെ ആപേക്ഷികതാ സിദ്ധാന്തങ്ങളുടെ മിക്ക പ്രവചനങ്ങളും നാം പരീക്ഷിച്ച് ബോധ്യപ്പെട്ടിട്ടുണ്ട്. എന്നാൽ ചില കാര്യങ്ങൾ നമുക്ക് 'പരീക്ഷിക്കാൻ' സാധിക്കില്ല. ഒരു സൈദ്ധാന്തിക പ്രവചനം സത്യമാണോ എന്ന് തെളിയിക്കാൻ കൃത്രിമമായി സാഹചര്യങ്ങൾ സൃഷ്ടിക്കുകയാണ് പരീക്ഷണത്തിൽ ചെയ്യുന്നത്. ഹിഗ്സ് ബോസോണിന്റെ കണ്ടെത്തലിന് കണികാപരീക്ഷണ ശാല എന്ന കൃത്രിമ സംവിധാനം ഉണ്ടാക്കിയത് ഒരു ഉദാഹരണമാണ്. പക്ഷേ ഗുരുത്വതരംഗങ്ങളെക്കുറിച്ച് ആപേക്ഷികത പറയുന്നത് അതിഭീമൻ പിണ്ഡമുള്ള വസ്തുക്കളുടെ ചലനവുമായി ബന്ധപ്പെട്ടാണ്. ഒരു നക്ഷത്രം എടുത്ത് ചുഴറ്റുന്നതോ ബ്ലാക്ഹോളിനെ എടുത്ത് കുലുക്കുന്നതോ ഒന്നും കൃത്രിമമായി സൃഷ്ടിക്കുക സാധ്യമല്ലല്ലോ. അവിടെ പരീക്ഷണം അല്ല, മറിച്ച് നിരീക്ഷണം മാത്രമേ സാധിയ്ക്കൂ. അതിന് മതിയായ സാഹചര്യങ്ങൾ പ്രപഞ്ചത്തിൽ സ്വാഭാവികമായി ഉണ്ടാകുന്നത് വരെ കാത്തിരിക്കേണ്ടിവരും. ഗുരുത്വതരംഗങ്ങളെ കാണാൻ, അവയെക്കുറിച്ചുള്ള സൈദ്ധാന്തിക പ്രവചനം നടന്നശേഷം നൂറ് വർഷങ്ങൾ കാത്തിരിക്കേണ്ടിവന്നു!
ഇനിയും ഞാൻ കാര്യത്തിലേയ്ക്ക് കടന്നില്ലല്ലോ എന്ന പരാതി കാണും. സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം എന്ന, കേൾക്കുമ്പോൾ അതിവിചിത്രമായ സിദ്ധാന്തത്തിലേയ്ക്ക് പെട്ടെന്ന് എടുത്ത് ചാടിയിട്ട് കാര്യമില്ല. അതിന് ചില മുന്നൊരുക്കങ്ങൾ കൂടിയേ തീരൂ. അതിനാണ് നാമിവിടെ ശ്രമിക്കുന്നത്. സാമാന്യ ആപേക്ഷികതയിലേയ്ക്ക് ഐൻസ്റ്റൈൻ എത്തിച്ചേരുന്നത് സമാനതാ സിദ്ധാന്തം (principle of equivalence) എന്ന മറ്റൊരു സിദ്ധാന്തത്തിൽ നിന്നാണ്.
നിങ്ങൾ ഒരു ലിഫ്റ്റിലാണ്. പതിനെട്ടാം നിലയിൽ നിന്നും താഴേയ്ക്കുള്ള വരവിനിടെ ഭാഗ്യം കൊണ്ട് ഈ ലിഫ്റ്റിന്റെ കെട്ട് പൊട്ടി എന്ന് സങ്കല്പിക്കുക. ചാവാൻ പോകുമ്പോഴും ഫിസിക്സ് പഠിയ്ക്കാനുള്ള താത്പര്യം ഉള്ള വിചിത്രജീവിയാണ് നിങ്ങൾ എന്നുകൂടി സങ്കല്പിച്ചുകൊണ്ട് ചോദിക്കട്ടെ, താഴേയ്ക്ക് വീഴുമ്പോൾ നിങ്ങൾക്ക് എന്താകും അനുഭവപ്പെടുക? ഒരു സ്പ്രിങ് ബാലൻസിൽ കല്ല് കെട്ടിത്തൂക്കിയിട്ട് അത് താഴേയ്ക്ക് വിട്ടാൽ വീഴുന്ന സമയത്ത് കല്ലിന്റെ ഭാരം പൂജ്യം കാണിക്കും. അതുപോലെ താഴേയ്ക്ക് വീഴുന്ന ആളിനും ഭാരമില്ലായ്മ അനുഭവപ്പെടും. അതായത് സ്വതന്ത്രമായി താഴേയ്ക്കുവീഴുക എന്ന ഫ്രീഫോൾ (free-fall) അവസ്ഥയിൽ ഗുരുത്വാകർഷണം നിങ്ങൾക്ക് അനുഭവപ്പെടില്ല. ഇതിനെ മറ്റൊരു രീതിയിൽ കൂടി ആലോചിക്കാം. നിങ്ങൾ ഒരു സ്പെയ്സ് ഷിപ്പിലാണ്. ബാഹ്യകാശത്തുകൂടി അത് സ്വതന്ത്രമായി നീങ്ങിക്കൊണ്ടിരിക്കുന്നു. ഷിപ്പിന്റെ എഞ്ചിൻ ഓഫാണ്. നിങ്ങൾ തീർത്തും ഭാരരഹിതമായി അതിനുള്ളിൽ പൊങ്ങിക്കിടക്കുന്നു. പെട്ടെന്ന് നിങ്ങൾ അതിന്റെ ഒരു ചുവരിലേയ്ക്ക് വലിയ്ക്കപ്പെടുന്നു. ഒന്നുകിൽ നിങ്ങളുടെ സ്പെയ്സ് ഷിപ്പിന്റെ എഞ്ചിൻ ഓണായി അത് accelerate ചെയ്യപ്പെട്ടതാണ് (നിർത്തിയിട്ടിരിക്കുന്ന ബസ് മുന്നോട്ടെടുക്കുമ്പോൾ സീറ്റിലേയ്ക്ക് അമർത്തപ്പെടുന്നതുപോലെ) അല്ലെങ്കിൽ നിങ്ങളുടെ സ്പെയ്സ് ഷിപ്പ് ഏതോ ആകാശഗോളത്തിന്റെ ഗ്രാവിറ്റിയുടെ പരിധിയിലേയ്ക്ക് കടന്നിരിക്കുന്നു. ആ ഗോളം നിങ്ങളിൽ ഗുരുത്വാകർഷണം ചെലുത്തുകയാണ്. ഇതിൽ ഏതാണ് സംഭവിച്ചിരിക്കുന്നത് എന്നറിയാൻ മാർഗമുണ്ടോ? ഇല്ല. സ്പെയ്സ് ഷിപ്പിനുള്ളിലിരുന്നുകൊണ്ട് പുറംലോകവുമായി ഏതെങ്കിലും രീതിയിൽ ബന്ധപ്പെടാതെ, അത് accelerate ചെയ്തതാണോ ഏതെങ്കിലും ഗുരുത്വാകർഷണ ബലത്തിന് വിധേയമായതാണോ എന്ന് കണ്ടെത്താൻ നിങ്ങൾക്ക് സാധിക്കില്ല. ഒരു പരീക്ഷണത്തിനും ഈ രണ്ട് പ്രഭാവങ്ങളേയും തമ്മിൽ വേർതിരിച്ചറിയാൻ പറ്റില്ല. ഇതാണ് സാമാനതാ സിദ്ധാന്തം.
അതായത്, ഒരു വസ്തുവിന് acceleration അഥവാ ത്വരണം സംഭവിക്കുന്നതും അതിൽ ഒരു ഗുരുത്വാകർഷബലം ചെലുത്തപ്പെടുന്നതും തമ്മിൽ യാതൊരു വ്യത്യാസവും ഇല്ല. അങ്ങനെയെങ്കിൽ ആപ്പിൾ താഴേയ്ക്ക് ത്വരണത്തിന് വിധേയമാകുന്നതാണ്, ഭൂമി അതിനെ ആകർഷിക്കുകയൊന്നും ചെയ്യുന്നില്ല എന്നാണെങ്കിലോ? ഗുരുത്വാകർഷണബലം പ്രയോഗിക്കാതെ തന്നെ, വേറെ ഏതെങ്കിലും കാരണം കൊണ്ടാണ് ആപ്പിൾ ത്വരണത്തിന് വിധേയമാകുന്നത് എങ്കിലോ? അപ്പോ, ഗുരുത്വാകർഷണ ബലം എന്നൊരു ബലമേ ഇല്ലെങ്കിലോ?
വളഞ്ഞ സ്ഥലകാലം
ഒരു വസ്തുവിന്റെ സ്ഥാനമോ ചലനമോ പറയുന്നതിനും പഠിക്കുന്നതിനും അതിനെ ഏതെങ്കിലും ഒരു റഫറൻസുമായി താരതമ്യം ചെയ്യേണ്ടതുണ്ട്. ഉദാഹരണത്തിന്, ഒരു പേപ്പറിൽ ഒരു മുത്ത് ഇരിക്കുന്നു. അതിന്റെ പേപ്പറിലെ സ്ഥാനം പറയാൻ, പേപ്പറിന്റെ ഒരു മൂലയെ കേന്ദ്രബിന്ദുവും അവിടന്ന് പരസ്പരം ലംബമായ രണ്ട് വക്കുകളെ അക്ഷങ്ങളായും എടുത്ത് ഒരു നിർദേശാങ്ക സംവിധാനം സങ്കല്പിക്കാം. ഇതിൽ ഇടത്തുനിന്ന് വലത്തേയ്ക്കുള്ള ദിശയെ x-ദിശ എന്നും താഴെ നിന്ന് മുകളിലേയ്ക്കുള്ള ദിശയെ y-ദിശ എന്നും വിളിക്കാം. ഇനി ആ മുത്തിന്റെ സ്ഥാനം പറയാൻ രണ്ട് ദൂരങ്ങൾ പറഞ്ഞാൽ മതി. ഈ രണ്ട് ദിശകളിലും ഈ മുത്ത്, കേന്ദ്രബിന്ദുവിൽ നിന്ന് എത്ര ദൂരെയാണ് എന്നാണ് അവ സൂചിപ്പിക്കുന്നത്. ഈ രണ്ട് അക്ഷങ്ങളുടെ ദിശയിലുള്ള ഏത് രണ്ട് ദൂരങ്ങൾ പറഞ്ഞാലും അത് ഏതെങ്കിലുമൊരു പ്രത്യേക ബിന്ദുവിന്റെ സ്ഥാനത്തെ സൂചിപ്പിക്കും. അവയെ ക്രമത്തിൽ (x,y) എന്നിങ്ങനെ എഴുതുകയാണ് പതിവ്. അതായത് ഓരോ ജോഡി (x,y)-യും ഒരു പ്രത്യേക സ്ഥാനമാണ്. അവയെ നിർദേശാങ്കങ്ങൾ (coordinates) എന്ന് വിളിക്കുന്നു. ഇപ്പോൾ പേപ്പർ പ്രതലത്തിലെ മുത്തിന്റെ സ്ഥാനം ഒരു ജോഡി സംഖ്യകൾ എന്ന ഗണിതരൂപം കൈവരിച്ചിരിക്കുന്നതായി കാണാം.
ഇനി ഒരു ഗണിതക്രിയയിൽ ഇതിലെ x-ഉം y-യും മാറുന്നു എങ്കിൽ അതിന്റെ അർത്ഥം എന്താണ്? x-ഉം y-യും സ്ഥാനത്തെ സൂചിപ്പിക്കുന്നു, അവ മാറിയാൽ സ്ഥാനം മാറുന്നു, സ്ഥാനം മാറുക എന്നാൽ അത് ചലനത്തെ സൂചിപ്പിക്കുന്നു. ഇങ്ങനെ നിർദേശാങ്കങ്ങളിലെ മാറ്റമായിട്ട് ചലനത്തെ നമുക്ക് വിശദീകരിക്കാനാകുന്നു. സ്ഥാനത്തേയും ചലനത്തേയും ഭൗതികശാസ്ത്രം കൈകാര്യം ചെയ്യുന്നത് ഇങ്ങനെയാണ്. പേപ്പറിന് പകരം ഒരു മുറിയിലെ ഈച്ചയുടെ ചലനമാണ് സൂചിപ്പിക്കേണ്ടത് എങ്കിൽ മുറിയുടെ ഒരു മൂലയെ കേന്ദ്രബിന്ദുവാക്കി, പരസ്പരം ലംബമായ മൂന്ന് അക്ഷങ്ങൾ സങ്കല്പിക്കാനാകും. പേപ്പർ എന്ന 2D വസ്തുവിന് രണ്ട് നിർദേശാങ്കങ്ങൾ മതിയായിരുന്നു. മുറി 3D ആയതിനാൽ നിർദേശാങ്കങ്ങളും മൂന്ന് വേണ്ടിവരും എന്നേയുള്ളു.

ഒരു 3D സ്പെയ്സിൽ മൂന്ന് സ്ഥാന നിർദേശാങ്കങ്ങളെയും സമയത്തേയും ബന്ധിപ്പിച്ച്, സമയം മാറുമ്പോൾ നിർദേശാങ്കങ്ങൾ എങ്ങനെ മാറുന്നു എന്ന് സൂചിപ്പിക്കുന്ന ഒരു ഗണിതസമവാക്യം ഉണ്ടെങ്കിൽ അത് ഒരു വസ്തുവിന്റെ ചലനത്തെ ഗണിതരൂപത്തിൽ ഒരു പേപ്പറിൽ വിശദീകരിക്കാനാകും.
നിർദേശാങ്കങ്ങൾ എന്ന സങ്കല്പത്തെ പരിചയപ്പെടുത്താനാണ് ഇത്രയും പറഞ്ഞത്. ഇപ്പോൾ കണ്ട, പരസ്പരം ലംബമായ അക്ഷങ്ങളെ ഉപയോഗിക്കുന്ന നിർദേശാങ്കരീതിയെ കാർട്ടേസ്യൻ രീതി (Cartesian system) എന്നാണ് വിളിക്കുന്നത്. എന്നാൽ എല്ലായ്പ്പോഴും ഈ രീതി തന്നെ തുടരണം എന്നില്ല. ഒരു വസ്തുവിന്റെ സ്ഥാനത്തെ കുറച്ച് സംഖ്യകളുടെ രൂപത്തിൽ സൂചിപ്പിക്കാനാകുന്ന ഏത് സമ്പ്രദായവും ഉപയോഗിക്കാം. സാഹചര്യത്തിന് ഏറ്റവും സൗകര്യപ്രദമായത് നമ്മൾ തെരെഞ്ഞെടുക്കും. ഉദാഹരണത്തിന് നമുക്കൊക്കെ ഏറേ പരിചിതമായ ഒരു നിർദേശാങ്ക സമ്പ്രദായമാണ് അക്ഷാംശവും രേഖാംശവും (latitude-longitude).
ഭൂമിയുടെ ഉപരിതലത്തിൽ സ്ഥാനവും ചലനവും പറയാൻ റഫറൻസായി നാമത് ഉപയോഗിക്കുന്നു. ഇത് പക്ഷേ കാർട്ടേസ്യൻ രീതിയല്ല പിൻതുടരുന്നത്. എന്താണ് പ്രശ്നം? കാർട്ടേസ്യൻ രീതിയിൽ പരസ്പരം ലംബമായ നേർദിശകളാണ് നമ്മൾ ഉപയോഗിച്ചത്. ഭൂമിയുടെ ഉപരിതലത്തിൽ ഇത് സാധ്യമാണോ? രേഖാശരേഖകൾ മധ്യരേഖാ പ്രദേശങ്ങളിൽ സമാന്തരമാണെങ്കിലും ഭൂമിയുടെ ഗോളാകൃതി കാരണം അവ ധ്രുവപ്രദേശങ്ങളിൽ വച്ച് കൂടിച്ചേരുന്നു. ഈ ഭൂമിയുടെ ഉപരിതലത്തിൽ ഒരു വലിയ ത്രികോണം വരച്ചിട്ട് അതിന്റെ മൂന്ന് കോണുകൾ അളന്ന് കൂട്ടിയാൽ 180 ഡിഗ്രി ആയിരിക്കില്ല, കൂടുതലുണ്ടാകും!
സ്കൂളിൽ അടിസ്ഥാന ജ്യാമിതീയ നിയമമായിട്ട് പഠിച്ച കാര്യമാണ് ത്രികോണത്തിലെ 180 ഡിഗ്രി! അത് ഇവിടെ ബാധകമല്ല. അതിനർത്ഥം സ്കൂളിൽ പഠിച്ച ഗണിതം പോരാ ഈ സാഹചര്യം കൈകാര്യം ചെയ്യാൻ. ഇവിടെ ഉപയോഗിക്കുന്നത് ഒരു വളഞ്ഞ നിർദേശാങ്കരീതിയാണ് (curved coordinates). അതിന് വളരെ സങ്കീർണമായ ചില ഗണിതസങ്കേതങ്ങൾ ഉപയോഗിക്കേണ്ടിവരും. അതിവിടെ പരിചയപ്പെടുത്താൻ നിർവാഹമില്ല. പക്ഷേ നിർദേശാങ്കസംവിധാനത്തിന്റെ അക്ഷങ്ങൾ വളയുന്നതും, എത്രത്തോളം വളയുന്നുണ്ട് എന്നതുമൊക്കെ സൂചിപ്പിക്കാൻ കൃത്യമായ ഗണിതോപകരണങ്ങൾ ഉണ്ട്. സ്കൂളിൽ പഠിച്ച യൂക്ലിഡിയൻ ജ്യാമിതിയ്ക്ക് (Euclidean geometry, പുരാതന ഗണിതജ്ഞനായ യൂക്ലിഡ് ആവിഷ്കരിച്ചത്) പകരം പത്തൊമ്പതാം നൂറ്റാണ്ടിൽ ബെൺഹാഡ് റീമാൻ എന്ന ഗണിതജ്ഞൻ ആവിഷ്കരിച്ച റീമാനിയൻ ജ്യാമിതിയാണ് അവിടെ ഉപയോഗിക്കുന്നത്.
ഗുരുത്വവും വളവും
ഗുരുത്വാകർഷണം പ്രവർത്തിക്കുന്ന രീതിയും മേൽപ്പറഞ്ഞ വളഞ്ഞ നിർദേശാങ്കരീതിയും തമ്മിൽ ചെറുതല്ലാത്ത ഒരു സാമ്യം ഐൻസ്റ്റൈന്റെ ശ്രദ്ധയിൽ പെട്ടു. നിങ്ങൾ രണ്ട് കൈകളിലായി രണ്ട് പന്തുകൾ എടുത്തിട്ട് അവയെ ഒരേസമയം താഴേയ്ക്ക് ഇടുന്നതായി സങ്കല്പിക്കുക. അവ ഗുരുത്വാകർഷണത്തിന് വിധേയമായി താഴേയ്ക്ക് വീഴുന്നു. അവ രണ്ടും സമാന്തരമായിട്ടാണ് വീഴുന്നത് എന്ന കാര്യത്തിൽ തർക്കമുണ്ടോ? ഇല്ലെങ്കിൽ നമുക്കൊന്ന് തർക്കിക്കേണ്ടിവരും. കാരണം, കാഴ്ചയ്ക്ക് അവ സമാന്തരമാണെങ്കിലും അവയെ രണ്ടിനേയും വലിക്കുന്നത് ഒരേ ബലമാണ്- ഭൂമിയുടെ ഗുരുത്വബലം. അത് പക്ഷേ ഭൂമിയുടെ കേന്ദ്രം എന്ന ഒറ്റ ബിന്ദുവിലേയ്ക്കാണ് വലിക്കുന്നത്. ഒരേ ബിന്ദുവിലേയ്ക്ക് പോകുന്ന രണ്ട് പന്തുകൾ സമാന്തരമാകാൻ തരമില്ലല്ലോ. ചെറിയ വീഴ്ചകളിൽ ഇത് അവഗണിക്കാവുന്നത്ര ചെറിയ പ്രഭാവമേ ഉണ്ടാക്കുന്നുള്ളു. പക്ഷേ സ്കൈ ഡൈവേഴ്സിനെപ്പോലെ വലിയ ഫ്രീഫോൾ നടത്തുന്നവർക്ക് ഇത് ഗണ്യമാണ്. താഴേയ്ക്ക് വീഴുന്തോറും അവർ പരസ്പരം അടുത്തുവരും. ഇത് മനസിലാക്കാൻ താഴെയുള്ള ചിത്രം നോക്കുക.
ഇനി ഭൂമിയുടെ ഉപരിതലം എന്ന വളഞ്ഞ പ്രതലത്തിലെ രണ്ട് രേഖാംശരേഖകളുടെ പോക്ക് ശ്രദ്ധിക്കൂ.
ഇവിടെ രണ്ട് പച്ച വരകളും മധ്യരേഖയിൽ (ചുവപ്പ്) നിന്ന് ഒരേ ദിശയിലാണ് പുറപ്പെടുന്നത്. രണ്ട് വരകളും മധ്യരേഖയ്ക്ക് ലംബവുമാണ്. പക്ഷേ മുകളിലേയ്ക്ക് പോകുന്തോറും അവ പരസ്പരം അടുക്കുന്നു. ധ്രുവത്തിലെത്തുമ്പോൾ അവ കൂട്ടിമുട്ടും. താഴേയ്ക്ക് വീഴുന്ന രണ്ടു പന്തുകളുടെ സഞ്ചാരപഥം ഭൂകേന്ദ്രത്തിൽ കൂട്ടിമുട്ടുന്നതുപോലെ!
ഈ ഒരു സാമ്യമാണ്, ഐൻസ്റ്റൈനെ ഗുരുത്വാകർഷണത്തേയും റീമാന്റെ വളഞ്ഞ ജ്യാമിതിയേയും കൂട്ടിക്കെട്ടാൻ പ്രേരിപ്പിച്ചത്. സ്പെയ്സ് എന്ന 3D സങ്കല്പത്തിന് പകരം, സ്പെയ്സും സമയവും ചേർന്ന സ്ഥലകാലം (spacetime) എന്ന 4D സങ്കല്പത്തിലാണ് അദ്ദേഹം അത് പ്രയോഗിച്ചത് എന്നേയുള്ളു. ഒന്നാലോചിച്ചേ, യൂക്ലിഡിന്റേതിൽ നിന്ന് വിട്ട് വളഞ്ഞൊരു ജ്യാമിതി സങ്കല്പിക്കാൻ തന്നെ സാധാരണ തലച്ചോറിന് ബുദ്ധിമുട്ടാണ്. 3D ലോകത്തോട് സമയം എന്ന അന്തോം കുന്തോമില്ലാത്ത സാധനം കൂടി ചേർത്ത് ഒറ്റ വസ്തുവായി കാണാനും സാധാരണ തലച്ചോറിന് ബുദ്ധിമുട്ടാണ്. ഐൻസ്റ്റൈന്റെ തലച്ചോറ് ഇതിൽ ഒന്നെടുത്ത് മറ്റേതിൽ അപ്ലൈ ചെയ്തു! ഹമ്പമ്പോ!! സയൻസിനെക്കുറിച്ച് വലിയ അറിവൊന്നും ഇല്ലാത്തവർക്ക് പോലും ഐൻസ്റ്റൈന്റെ പേര് പരിചിതമാകുന്നത് ഇതുകൊണ്ടാണ്. ബയങ്കരമാന ആൾ!! (trivia: സ്ഥലവും സമയവും കൂട്ടിച്ചേർത്ത് സ്ഥലകാലം എന്ന ഒറ്റ വസ്തുവാക്കി മാറ്റിയത് സത്യത്തിൽ ഐൻസ്റ്റൈനല്ല. അദ്ദേഹത്തിന്റെ തന്നെ വിശേഷ ആപേക്ഷികതാ സിദ്ധാന്തത്തിൽ നിന്ന് പ്രചോദനം ഉൾക്കൊണ്ട്, അദ്ദേഹത്തിന്റെ മുൻ അധ്യാപകനായിരുന്ന ഹെർമാൻ മിങ്കോവ്സ്കി ആണ് അത് ചെയ്തത്. അതുകൊണ്ട് ആ 4D സ്പെയ്സിനെ മിങ്കോവ്സ്കി സ്പെയ്സ് എന്ന് വിളിക്കാറുണ്ട്)
ഇനി നമ്മൾ നേരിട്ട് ഐൻസ്റ്റൈന്റെ അവസാന അനുമാനത്തിലേയ്ക്ക് ചാടുകയാണ്. മനസിലാവില്ല എന്നറിഞ്ഞുകൊണ്ട് തന്നെ, സാമാന്യ ആപേക്ഷികതയുടെ ആണിക്കല്ലായ ഐൻസ്റ്റൈൻ ഫീൽഡ് സമവാക്യങ്ങൾ ഒന്ന് കാണിക്കാം.
ഇതിപ്പോ സമവാക്യങ്ങൾ എന്ന് പറഞ്ഞിട്ട് ഒന്നേയുള്ളല്ലോ എന്നാരെങ്കിലും വിചാരിക്കുന്നു എങ്കിൽ ക്ഷമിക്കുക. മൊത്തം പത്ത് സമവാക്യങ്ങളാണ് മുകളിൽ കാണുന്നത്. പ്രാഞ്ചിയേട്ടൻ പറഞ്ഞപോലെ, ഇദിനൊക്കെ ബയങ്കര അർത്ഥമാണ്!
ഈ സമവാക്യം എന്താണ് പറയുന്നത് എന്ന് ചുരുക്കി പറയാം. ഇതിൽ ഇടതുവശത്ത് കാണുന്ന ചിഹ്നങ്ങളെല്ലാം റീമാനിയൻ ജ്യാമിതി അനുസരിച്ച് ഒരു നിർദേശാങ്കസംവിധാനത്തിലെ വളവുകളെക്കുറിച്ചാണ് സംസാരിക്കുന്നത്. ഇടതുവശത്തെ T എന്നത്, ദ്രവ്യം ഏതൊക്കെ അളവിൽ എവിടെയൊക്കെ വിതരണം ചെയ്യപ്പെട്ടിരിക്കുന്നു എന്നതിനെ സൂചിപ്പിക്കുന്നു. ആപേക്ഷികതയിൽ ഊർജവും ദ്രവ്യവും ഒന്ന് തന്നെ ആണെന്നതും (E = mc2) ഓർമിക്കണം. ഈ രണ്ട് കാര്യങ്ങളും ഒരു സമവാക്യത്തിന്റെ അപ്പുറവും ഇപ്പുറവും നിൽക്കുന്നു എങ്കിൽ അവ തമ്മിൽ പരസ്പരം ബന്ധപ്പെട്ടിരിക്കുന്നു എന്നാണല്ലോ അർത്ഥം. അതായത്, ദ്രവ്യം എങ്ങനെ വിതരണം ചെയ്യപ്പെട്ടിരിക്കുന്നു എന്നതനുസരിച്ച് ചുറ്റുമുള്ള സ്ഥലകാലം വളയുന്നു എന്ന്! ഇതാണ് ഒറ്റവാക്യത്തിൽ പറഞ്ഞാൽ സാമാന്യ ആപേക്ഷികത.
4D ആയ ഈ ലോകത്തിൽ ഇരിക്കുന്ന പിണ്ഡമുള്ള ഓരോ വസ്തുവും അതിന് ചുറ്റുമുള്ള സ്ഥലകാലത്തെ വളയ്ക്കുന്നു. എത്രത്തോളം പിണ്ഡം കൂടുതലുണ്ടോ അത്രത്തോളം കൂടുതൽ അത് സ്ഥലകാലത്തെ വളയ്ക്കുന്നു. യാതൊരു ബാഹ്യബലവും പ്രവർത്തിക്കാത്ത പക്ഷം ചലിക്കുന്ന വസ്തുക്കൾ നേർരേഖയിൽ സഞ്ചരിച്ചുകൊണ്ടേയിരിക്കും. പക്ഷേ ആ നേർരേഖ സ്ഥിതി ചെയ്യുന്നത് ഒരു വളഞ്ഞ സ്ഥലകാലത്തിലാണെങ്കിലോ? ഒരു പേപ്പർ എടുത്ത് മേശപ്പുറത്ത് വച്ച് അതിൽ ഒരു നേർരേഖ വരയ്ക്കുകയും, പിന്നെ ആ പേപ്പറിനെ ചുരുട്ടി ഒരു കുഴലാക്കുകയും ചെയ്താൽ, ഇപ്പോൾ അതിൽ കാണുന്നത് നേർരേഖയാണോ വളഞ്ഞ രേഖയാണോ? അത് വളഞ്ഞ് കാണുന്ന ഒരു നേർരേഖയാണ് എന്നേ പറയാനാകൂ. അതുപോലെ ഈ പ്രപഞ്ചത്തിൽ ഗുരുത്വാകർഷണത്തിന് മാത്രം വിധേയമായി വളഞ്ഞോ കറങ്ങിയോ ഒക്കെ സഞ്ചരിക്കുന്ന സകല വസ്തുക്കളും സത്യത്തിൽ നേർരേഖയിൽ ആണ് സഞ്ചരിക്കുന്നത്. ഭൂമിയും ചന്ദ്രനും ഗ്രഹങ്ങളും ഒക്കെ നേർരേഖയിലാണ് സഞ്ചരിക്കുന്നത്. ആ നേർരേഖകൾ വളഞ്ഞ സ്ഥലകാലത്തിലാണ് എന്നേയുള്ളു. അതായത് ഗുരുത്വാകർഷണം എന്നൊരു ബലമില്ല!!!
ഇത് പോരല്ലോ, ഒരിയ്ക്കൽ കൂടി പറയണ്ടേ? അതായത് ഗുരുത്വാകർഷണം എന്നൊരു ബലം ഇല്ല. വസ്തുക്കൾ സ്വാഭാവികമായി നേർരേഖയിലാണ് സഞ്ചരിക്കുന്നത്. പക്ഷേ ആ നേർരേഖ വളഞ്ഞ സ്ഥലകാലത്തിൽ ആയതിനാൽ പലപ്പോഴും വളഞ്ഞ് കാണപ്പെടുന്നു. സ്ഥലകാലത്തെ വളയ്ക്കുന്നത് പിണ്ഡമുള്ള വസ്തുക്കളുടെ (ദ്രവ്യത്തിന്റെ) സാന്നിദ്ധ്യമാണ്. അതുകൊണ്ട് പിണ്ഡമുള്ള മറ്റ് വസ്തുക്കളാണ് ഒരു വസ്തുവിന്റെ പാതയെ വളയ്ക്കുന്നത് എന്ന് നമുക്ക് തോന്നുന്നു. അതുകൊണ്ട് പിണ്ഡമുള്ള വസ്തുക്കൾ പരസ്പരം ആകർഷിക്കുന്നതായും, ഗുരുത്വാകർഷണം എന്നൊരു ബലം ഉണ്ടെന്നും നാം കരുതുന്നു. (ഈ പാരഗ്രാഫ് ഒരിയ്ക്കൽ കൂടി വായിച്ചാൽ ഐൻസ്റ്റൈന്റെ സാമാന്യ ആപേക്ഷികതയും ന്യൂട്ടന്റെ ഗുരുത്വാകർഷണ സിദ്ധാന്തവും തമ്മിലുള്ള ബന്ധം പിടികിട്ടും).
സാമാന്യ ആപേക്ഷികത ഗുരുത്വാകർഷണം എന്നൊരു ബലത്തെ നിരാകരിക്കുന്നു. സ്ഥലകാലവക്രത കാരണം കാണപ്പെടുന്ന ഒരു അനുഭവം മാത്രമാണ് ആ ബലം. ഇത് മനസിൽ ചിത്രീകരിക്കാനുള്ള എളുപ്പത്തിന് വലിച്ച് കെട്ടിയ ഒരു ഇലാസ്റ്റിക് തോർത്തിൽ നടുക്ക് കനമുള്ള ഒരു ഗോളം വെയ്ക്കുന്നതായി സങ്കല്പിക്കുക. നടുക്ക് ഒരു കുഴി രൂപപ്പെടുന്നു. ഇനി ആ ഗോളത്തിന്റെ പരിസരത്തുകൂടി മറ്റൊരു ചെറിയ ബോൾ ഉരുട്ടിവിട്ടാൽ എന്തുസംഭവിക്കും? തോർത്തിലെ കുഴിവ് കാരണം അതിന്റെ പാത മാറും.
ഒരുപാട് അടുത്തുകൂടിയാണെങ്കിൽ, ബോൾ ആ കുഴിയിൽ പെട്ട് ഗോളത്തിന് ചുറ്റും കറങ്ങാൻ തുടങ്ങും. ഏതാണ്ട് ഇതുതന്നെയാണ് ഗുരുത്വാകർഷണബലമെന്ന തോന്നലിനും കാരണമാകുന്നത്. പക്ഷേ ഈ ഉദാഹരണം പറയുന്നിടത്തെല്ലാം ഒരു മുന്നറിയിപ്പ് കൂടി കൊടുക്കേണ്ടതുണ്ട്. ഇതൊരു ഉപമ മാത്രമാണ്. നെടുകേയും കുറുകേയും രണ്ട് തരം ഇഴകളുള്ള തോർത്തിന് പകരം നാല് തരം ഇഴകൾ ഉള്ളതാണ് സ്ഥലകാലം. അതിൽ ഒരു ഇഴയാകട്ടെ സമയം ആണ്. അതിനകത്താണ് ഈ 'വളവ്' ഉണ്ടാകുന്നത്. വളവ് എന്ന വാക്ക് മനസിൽ കൊണ്ടുവരുന്നതുപോലുള്ള ഒരു രൂപമേ ആകില്ല ആ സ്ഥലകാലവളവിന്. ഇതിനപ്പുറം വ്യക്തമായി അത് പറയാൻ എനിയ്ക്ക് അറിയുകയും ഇല്ല.
ഇനി നമുക്ക് ലേഖനപരമ്പരയുടെ ഒന്നാം ഭാഗത്തിൽ വച്ച് ഉത്തരമില്ലാതെ നിർത്തിയ ചോദ്യത്തിലേയ്ക്ക് മടങ്ങിവരാം. സൂര്യൻ അപ്രത്യക്ഷമായശേഷമുള്ള എട്ട് മിനിറ്റുകൾ ഭൂമിയുടെ അവസ്ഥ എന്തായിരിക്കും? അത് ഓർബിറ്റിൽ തുടരുമോ തെറിച്ചുപോകുമോ?
ചിന്തിക്കാനുള്ള എളുപ്പത്തിന് മേൽപ്പറഞ്ഞ തോർത്തിലാണ് സൂര്യനും ഭൂമിയും എന്ന് കരുതുക. സൂര്യൻ പെട്ടെന്ന് ഇല്ലാതായാൽ, അത് ഉണ്ടാക്കിയ സ്ഥലകാലക്കുഴി പടേന്ന് നിവരും. വലിച്ചുകെട്ടിയ റബ്ബർഷീറ്റിൽ വച്ച ഒരു ഗോളം പെട്ടെന്ന് എടുത്ത് മാറ്റിയാൽ അത് ആ ഷീറ്റിൽ ഒരു വിറയൽ ഉണ്ടാക്കുന്നതുപോലെ, അപ്രത്യക്ഷമാകുമ്പോൾ സൂര്യൻ കുഴിച്ചുവെച്ചിരുന്ന സ്ഥലകാലം നിവരുകയും അതൊരു തരംഗം (ഓളം) പോലെ ചുറ്റും പടരുകയും ചെയ്യും. ഇത് പക്ഷേ റബ്ബർ ഷീറ്റ് കണ്ട പരിചയം വച്ച് അങ്ങ് വെറുതേ പറയുന്നതല്ല, ഐൻസ്റ്റൈന്റെ ഫീൽഡ് സമവാക്യങ്ങൾ അനുസരിച്ച് ഈ തരംഗചലനം കണക്കാക്കിയെടുക്കാനാകും. ഈ തരംഗം സ്ഥലകാലം എന്ന 4D ലോകത്താണ് പടരുന്നത് എന്ന് പ്രത്യേകം പറയണ്ടല്ലോ അല്ലേ? ഇതാണ് ഗുരുത്വതരംഗം അഥവാ ഗ്രാവിറ്റേഷണൽ വേവ്! ഇവയുടെ വേഗത പ്രകാശവേഗതയ്ക്ക് തുല്യമായിരിക്കും എന്നാണ് ഐൻസ്റ്റൈൻ സമവാക്യങ്ങൾ പ്രവചിക്കുന്നത്. ഇതോടെ പ്രശ്നത്തിന് പരിഹാരമായിരിക്കുന്നു. സൂര്യൻ ഇല്ലാതാകുമ്പോൾ ഉണ്ടാകുന്ന സ്ഥലകാല ഓളങ്ങൾ ഭൂമിയിലെത്താൻ എട്ട് മിനിറ്റ് സമയമെടുക്കും. അപ്പോൾ ഭൂമിയുടെ നേർരേഖാപാതയുടെ വളവ് നിവരും. അതോടെ അത് ഓർബിറ്റിൽ നിന്നും തെറിച്ചുപോകുന്നതുപോലെ കാണപ്പെടും. അതായത് സൂര്യൻ അപ്രത്യക്ഷമായിക്കഴിഞ്ഞാലും എട്ട് മിനിറ്റ് കൂടി ഭൂമി ഓർബിറ്റിൽ തന്നെ ഉണ്ടാകും.
എന്നാൽ ഗുരുത്വതരംഗങ്ങൾ ഉണ്ടാകാൻ സൂര്യൻ അപ്രത്യക്ഷമാകണമെന്നൊന്നും ഇല്ല. പിണ്ഡമുള്ള ഒരു വസ്തു ക്രമമായി ചലിച്ചാൽ, കറങ്ങുകയോ വിറയ്ക്കുകയോ ചെയ്താൽ, ചുറ്റും ഓളങ്ങൾ ഉണ്ടാകുമെന്ന് ഊഹിക്കാൻ ബുദ്ധിമുട്ടില്ലല്ലോ. പക്ഷേ ആ വസ്തുവിന്റെ പിണ്ഡം, ചലനത്തിന്റെ സ്വഭാവം തുടങ്ങിയവ അനുസരിച്ചായിരിക്കും ആ ഗുരുത്വതരംഗങ്ങളുടെ ശക്തിയും സ്വഭാവവും. അത്യധികം ഭീമമായ ഊർജനിലയിലുള്ള പ്രതിഭാസങ്ങൾക്ക് മാത്രമേ ഒരുപാട് ദൂരേയ്ക്ക് സഞ്ചരിക്കാനും അളക്കപ്പെടാനും മാത്രം ശേഷിയുള്ള തരംഗങ്ങൾ ഉണ്ടാക്കാനാകൂ. അത് അത്ര സാധാരണമല്ലാത്തതിനാലാണ് ഒരു നൂറ്റാണ്ട് കാലം ഇവയെ നേരിട്ട് കാണുന്നതിന് ശാസ്ത്രലോകം കാത്തിരിക്കേണ്ടി വന്നത്.
ഗുരുത്വതരംഗങ്ങളെ പിടികൂടൽ
1915-ൽ ഐൻസ്റ്റൈൻ തന്റെ സാമാന്യ അപേക്ഷികതാ സിദ്ധാന്തം പ്രസിദ്ധീകരിച്ചു. എന്നാൽ അടുത്ത വർഷം, 1916-ലാണ് അതിന്റെ ഒരു അനന്തരഫലമായി ഗുരുത്വതരംഗങ്ങളുടെ അസ്തിത്വം പ്രവചിക്കുന്നത്. ഭാരമുള്ള വസ്തുക്കൾ അതിനാനുപാതികമായി അവയ്ക്ക് ചുറ്റുമുള്ള സ്ഥലകാലത്തെ വളയ്ക്കുന്നു. ഇവ ചലിക്കുമ്പോൾ ഈ വളയലും സ്ഥലകാലത്തിലൂടെ സഞ്ചരിക്കുമല്ലോ. എന്നാൽ ചില സാഹചര്യങ്ങളിൽ ഭാരിച്ച വസ്തുക്കളുടെ ചലനം ഉണ്ടാക്കുന്ന വക്രതാ വ്യത്യാസം ഒരു തരംഗമെന്നപോലെ പ്രകാശവേഗത്തിൽ പുറത്തേയ്ക്ക് പ്രക്ഷേപണം ചെയ്യപ്പെടും. ഇവയാണ് ഗുരുത്വതരംഗങ്ങൾ. നിങ്ങൾ ഒരു സുഹൃത്തിനോടൊപ്പം കുളത്തിൽ രണ്ടറ്റത്തായി ഇറങ്ങി നിന്നിട്ട് ഒരിടത്ത് നിന്ന് ഓളങ്ങൾ ഉണ്ടാക്കിക്കൊണ്ടിരിക്കുന്നു എന്ന് കരുതുക. ആ ഓളങ്ങൾ സഞ്ചരിച്ച് സുഹൃത്തിന്റെ അടുത്ത് എത്തുമ്പോൾ അയാൾക്ക് അനുഭവപ്പെടുന്നത് എന്തായിരിക്കും? തനിയ്ക്ക് ചുറ്റുമുള്ള വെള്ളത്തിൽ അയാൾക്ക് ഇളക്കങ്ങൾ കാണാനാകും. ഇതുപോലെ പ്രപഞ്ചത്തിൽ ഒരിടത്ത് നിന്ന് പുറപ്പെടുന്ന ഗുരുത്വതരംഗങ്ങൾ നമ്മുടെ അടുത്തെത്തുമ്പോൾ ഇത്തരം ഇളക്കങ്ങളാകും നമ്മളും കാണുക. പ്രധാനവ്യത്യാസം, ആ ഇളക്കങ്ങൾ സംഭവിക്കുന്നത് സ്ഥലകാലത്തിൽ ആയിരിക്കും എന്നതാണ്. അതായത് വസ്തുക്കൾക്കിടയിലുള്ള അകലം ഒരു താളത്തിൽ കൂടുകയും കുറയുകയും ചെയ്തുകൊണ്ടിരിക്കും. ആ താളം, നമ്മൾ നിരീക്ഷിക്കുന്ന ഗുരുത്വതരംഗത്തിന്റെ ഫ്രീക്വൻസി അനുസരിച്ചിരിക്കും.
പക്ഷേ ഗുരുത്വതരംഗങ്ങൾ ഉണ്ടാക്കുന്ന പ്രഭാവം നേരിട്ട് നിരീക്ഷിക്കുന്നതിൽ ചില വലിയ വെല്ലുവിളികൾ ഉണ്ട്. സൈദ്ധാന്തികമായി ചിന്തിച്ചാൽ, ഒരു നക്ഷത്രത്തെ ചുറ്റുന്ന ഗ്രഹം പോലും ചുറ്റുമുള്ള സ്ഥലകാലത്തിൽ ഗുരുത്വതരംഗങ്ങൾ ഉണ്ടാക്കുന്നുണ്ട്. പക്ഷേ നേരത്തേ പറഞ്ഞ ഇലാസ്റ്റിക് ഷീറ്റിൽ ഒരു ഉറുമ്പ് നടക്കുന്നതുപോലെ, തീരെ ദുർബലമായ ഒരു പ്രഭാവമേ അതുണ്ടാക്കൂ. പ്രഭാവം ചെറുതാകുന്തോറും അവയുടെ അളക്കലിന് കൂടുതൽ സവേദനക്ഷമതയുള്ള ഉപകരണങ്ങൾ വേണ്ടിവരും. ലോറിയുടേയും മറ്റും ഭാരമളക്കാനുള്ള വെയ്ബ്രിഡ്ജുകളിൽ നമുക്ക് സ്വർണമാലയുടെ ഭാരം അറിയാൻ കഴിയില്ലല്ലോ. കാരണം വെയ്ബ്രിഡ്ജുകൾക്ക് അത്ര ചെറിയ ഭാരം അളക്കാനുള്ള വേദനക്ഷമത ഇല്ല. ഗണ്യമായ ഇളക്കങ്ങൾ ഉണ്ടാകണമെങ്കിൽ ന്യൂട്രോൺ നക്ഷത്രങ്ങൾ, ബ്ലാക് ഹോളുകൾ തുടങ്ങി അതിഭീമൻ പിണ്ഡവും അതുകൊണ്ട് തന്നെ സ്പെയ്സ്ടൈമിൽ 'നല്ല പിടിപാടുമുള്ള' ആരെങ്കിലും വിചാരിക്കണം. പക്ഷേ ഇവയാകട്ടെ ഭൂമിയിൽ നിന്നും അതിവിദൂരതകളിലാണ് സ്ഥിതി ചെയ്യുന്നത്. ഗുരുത്വതരംഗങ്ങൾ ഉണ്ടാക്കുന്ന പ്രഭാവം സ്രോതസ്സിൽ നിന്നുള്ള ദൂരത്തിന്റെ വർഗത്തിന് വിപരീത അനുപാതത്തിലായിരിക്കും. അതായത് ദൂരം രണ്ട് മടങ്ങാണെങ്കിൽ അതിന്റെ പ്രഭാവം നാലിലൊന്നായി കുറയും. അതുകൊണ്ട് തന്നെ ഇവകളിൽ നിന്നുള്ള ഇളക്കം ഭൂമിയിൽ ഉണ്ടാക്കുന്ന പ്രഭാവം വളരെ വളരെ ചെറുതായിരിക്കും എന്നാണ് സമവാക്യങ്ങൾ പ്രവചിക്കുന്നത്. കൃത്യമായി പറഞ്ഞാൽ കിലോമീറ്ററുകൾ വലിപ്പമുള്ള ഒരു വസ്തുവിന്റെ നീളത്തിൽ, ഒരു ആറ്റത്തിന്റെ പത്തുകോടിയിൽ ഒരംശം മാത്രമേ വ്യത്യാസം വരാൻ സാധ്യതയുള്ളൂ. ഇത്രയും നിസ്സാരമായ ഒരു പ്രഭാവം നേരിട്ട് കാണുക അത്ര എളുപ്പമല്ലല്ലോ.
പരോക്ഷമായ തെളിവ്
സാമാന്യ ആപേക്ഷികതാ സിദ്ധാന്തം പരീക്ഷണ-നിരീക്ഷണങ്ങളിലൂടെ സ്ഥിരീകരിക്കാൻ എളുപ്പമായിരുന്നു. 1919-മുതൽ 1960-വരെ നടന്ന നിരവധി പരീക്ഷണങ്ങൾ ആപേക്ഷികതാ സിദ്ധാന്തം പറയുന്ന പ്രപഞ്ചചിത്രം ശരിയാണ് എന്ന് തന്നെ അടിവരയിട്ട് പറഞ്ഞു. പക്ഷേ, ഗുരുത്വതരംഗങ്ങളുടെ അസ്തിത്വം അവയുടെ അതിസൂക്ഷ്മസ്വഭാവം കൊണ്ട് തന്നെ പെട്ടെന്ന് വഴങ്ങുന്ന ഒന്നായിരുന്നില്ല. എന്നാൽ 1974-ൽ ഗുരുത്വതരംഗങ്ങളെ പരോക്ഷമായി സ്ഥിരീകരിക്കുന്ന ഒരു പഠനം പുറത്തുവന്നു.
പരസ്പരം ചുറ്റുന്ന രണ്ട് ന്യൂട്രോൺ നക്ഷത്രങ്ങളെക്കുറിച്ച് റസൽ ഹൾസ്, ജോസഫ് ടെയ്ലർ എന്നീ രണ്ട് അമേരിക്കൻ ശാസ്ത്രജ്ഞർ നടത്തിയ ഒരു കണ്ടെത്തലായിരുന്നു അത്. പരസ്പരം ചുറ്റുന്നതിനിടെ ഈ രണ്ട് ന്യൂട്രോൺ നക്ഷത്രങ്ങളും അടുത്തടുത്ത് വരുന്നുണ്ടായിരുന്നു. ഇതിനെ ഓർബിറ്റൽ ക്ഷയം (orbital decay) എന്നാണ് വിളിക്കുന്നത്. എഞ്ചിൻ പവർ കുറയുമ്പോൾ ഒരു വിമാനം താഴ്ന്നുവരുന്നതുപോലെ ഒരു പ്രഭാവമാണിത്. അതായത്, ചുറ്റുന്നതിനിടെ ഈ നക്ഷത്രങ്ങളുടെ ഊർജം നഷ്ടപ്പെടുന്നു എന്ന് വേണം കരുതാൻ. ഈ ഊർജം ഏത് വഴിയ്ക്കാണ് പോകുന്നത് എന്നറിയാൻ അവരവിടെ ഗുരുത്വതരംഗങ്ങളുടെ സഹായം തേടി. ആപേക്ഷികതയുടെ സമവാക്യങ്ങൾ പ്രയോഗിച്ചാൽ, ഗുരുത്വതരംഗങ്ങൾ ഇവയോടൊപ്പം ഊർജവും വഹിക്കുന്നുണ്ട് എന്ന് കാണാം. ന്യൂട്രോൺ നക്ഷത്രങ്ങൾ അതിഭീമൻ പിണ്ഡം ഉള്ളവയാണ്. അവ പരസ്പരം ചുറ്റുമ്പോൾ ഗുരുത്വതരംഗങ്ങളുടെ രൂപത്തിൽ എത്രത്തോളം ഊർജം പുറത്തുപോകുന്നുണ്ട് എന്നൊരു കണക്കൂകൂട്ടൽ അവർ നടത്തിനോക്കി. അത്രയും ഊർജം ആ നിരക്കിൽ നഷ്ടപ്പെട്ടാൽ അവയുടെ ഓർബിറ്റ് എങ്ങനെ വ്യത്യാസപ്പെടും എന്ന മറ്റൊരു കണക്കുകൂട്ടൽ കൂടി നടത്തുമ്പോൾ, അത് നമുക്ക് നേരിട്ട് നിരീക്ഷിക്കാവുന്ന ഓർബിറ്റൽ ക്ഷയത്തിന് തുല്യമാണെന്ന് അവർ കണ്ടെത്തി. ഈ കണ്ടെത്തലിന് ഹൾസ്-ടെയ്ലർ ജോഡികൾക്ക് 1993-ലെ നോബൽ സമ്മാനം നൽകപ്പെട്ടു.
പക്ഷേ എന്തൊക്കെ പറഞ്ഞാലും ന്യൂട്രോൺ നക്ഷത്രങ്ങളുടെ കാര്യത്തിൽ ഒരു പരോക്ഷമായ അനുകൂലവാദം മാത്രമേ ഗുരുത്വതരംഗങ്ങൾക്ക് ലഭിച്ചിരുന്നുള്ളു. അവയെ നേരിട്ട് നിരീക്ഷിക്കുക, അതായത് നാം കാണുന്ന വസ്തുക്കളിലൂടെ അത് കടന്നുപോകുമ്പോൾ ഉണ്ടാകുന്ന പ്രഭാവം നേരിട്ട് അളക്കുക എന്നത് അപ്പോഴും സ്വപ്നം മാത്രമായി അവശേഷിച്ചു. അവിടെയാണ് LIGO രംഗപ്രവേശം ചെയ്യുന്നത്.
LIGO അഥവാ ഗുരുത്വതരംഗത്തിനൊരുക്കിയ വല
Laser Interferometer Gravitational-wave Observatory എന്നതിന്റെ ചുരുക്കപ്പേരാണ് ലൈഗോ. അതിന്റെ ചരിത്രപരമായ വികാസത്തിന്റെ കഥ ഉപേക്ഷിച്ചിട്ട് അതിലെ ശാസ്ത്രം മാത്രമേ തത്കാലം നമ്മൾ ചർച്ച ചെയ്യുന്നുള്ളൂ, അതും വളരെ ചുരുക്കി. ലൈഗോയുടെ മുഴുവൻ പേരിലെ interferometer എന്ന ഭാഗമാണ് ഇവിടെ ഉപയോഗിക്കുന്ന അടിസ്ഥാന ടെക്നിക്ക്. അത് വളരെ ലളിതമാണ്. ഒരു ലേസർ രശ്മിയെ നാം രണ്ട് വ്യത്യസ്ത ബീമുകളായി വിഭജിക്കുന്നു. എന്നിട്ട് അവയെ പരസ്പരം ലംബമായ രണ്ട് വ്യത്യസ്ത പാതകളിലൂടെ പരമാവധി ദൂരം സഞ്ചരിക്കാൻ അനുവദിക്കുകയും, കണ്ണാടികൾ ഉപയോഗിച്ച് പ്രതിഫലിപ്പിച്ച് തിരിച്ചുകൊണ്ടുവരികയും ചെയ്യുന്നു. ഇവ പരസ്പരം പിരിഞ്ഞ ഭാഗത്ത് വെച്ച് പിന്നേയും കൂടിച്ചേരുമ്പോൾ എന്ത് സംഭവിക്കുന്നു എന്നാണ് നാം നിരീക്ഷിക്കുന്നത്.
ലേസർ രശ്മികൾ എന്നാൽ അടിസ്ഥാനപരമായി വൈദ്യുതകാന്തിക തരംഗങ്ങൾ ആണെന്നറിയാമല്ലോ. തരംഗങ്ങൾ തമ്മിൽ കൂടിക്കലരുന്ന പ്രക്രിയയെയാണ് ഇന്റർഫറൻസ് എന്ന് വിളിക്കുന്നത്. തരംഗങ്ങൾ തമ്മിൽ കൂടിക്കലരുമ്പോൾ അവയുടെ ഉയർന്ന ഭാഗങ്ങളും താഴ്ന്ന ഭാഗങ്ങളും കൃത്യമായി പരസ്പരം ചേർന്നുവന്നാൽ അത് കുറച്ചുകൂടി ശക്തികൂടിയ ഒരു തരംഗത്തിനായിരിക്കും രൂപം കൊടുക്കുക. ഇതിനെ തരംഗശാക്തീകരണം (constructive interference) എന്ന് വിളിക്കാം. ഇനി ഒരു തരംഗത്തിന്റെ താഴ്ച മറ്റൊന്നിന്റെ ഉയർച്ചയുമായാണ് ചേരുന്നത് എങ്കിൽ തരംഗങ്ങൾ പരസ്പരം ഇല്ലാതാക്കപ്പെടും. ഇതാണ് തരംഗനാശനം (destructive interference). താഴത്തെ ചിത്രം നോക്കുക.
ഒരേ പ്രകാശരശ്മിയെയാണ് നാം രണ്ടായി വിഭജിക്കുന്നത്. അതുകൊണ്ട് തന്നെ ഇവ ഒരേ ദൂരം സഞ്ചരിച്ച് വീണ്ടും കൂടിച്ചേർന്നാൽ അവയുടെ ഉയർച്ചതാഴ്ചകൾ ഒരേ സ്ഥാനത്തായിട്ടായിരിക്കും വന്നുചേരുന്നത്. ഇവയിലേതെങ്കിലും ഒരു രശ്മി സഞ്ചരിക്കുന്ന ദൂരത്തിൽ വ്യത്യാസം വന്നാൽ ഈ കണക്ക് തെറ്റും. ഉയർച്ചതാഴ്ചകൾ ചേരുംപടി ചേരാതെ ഒരു ഇന്റർഫറൻസ് പാറ്റേൺ സൃഷ്ടിക്കപ്പെടും. ഇതിൽ ഒരു സാധ്യത ഒളിഞ്ഞുകിടപ്പുണ്ട്. പരസ്പരം ലംബമായ ദിശകളിൽ സഞ്ചരിച്ച് വരുന്ന പ്രകാശരശ്മികൾ തമ്മിൽ കൂടിച്ചേരാൻ അനുവദിക്കുകയാണ് നമ്മൾ. പെട്ടെന്ന് ഈ ഉപകരണത്തിലൂടെ ഒരു ഗുരുത്വതരംഗം കടന്നുപോകുന്നു എങ്കിലോ? രണ്ട് ദിശകളിലും സ്ഥലകാലം രണ്ട് രീതിയിലായിരിക്കും ഇളക്കപ്പെടുന്നത്. അതായത് പ്രകാശരശ്മികൾ സഞ്ചരിക്കുന്ന ദൂരങ്ങൾ തമ്മിൽ വ്യത്യാസം വരും. എത്രത്തോളം വ്യത്യാസം വന്നിട്ടുണ്ട് എന്നതനുസരിച്ച് ഇന്റർഫറൻസ് പാറ്റേൺ മാറും.
ഇത് തന്നെയാണ് LIGO-യും ഉപയോഗപ്പെടുത്തുന്നത്. ഇവിടെ വിഭജിക്കപ്പെടുന്ന ലേസർ രശ്മികൾ പരസ്പരം ലംബമായ ദിശകളിൽ 4 കിലോമീറ്റർ സഞ്ചരിച്ച് മടങ്ങിയെത്തുന്നു. ചെറിയ ദൂരവ്യത്യാസം പോലും അളക്കാൻ കഴിയുന്ന സംവേദനക്ഷമത കൈവരിക്കാനാണ് ഇത്രയും നീളമുള്ള സംവിധാനം വേണ്ടിവരുന്നത്. ഇതുപോലെ രണ്ട് LIGO ഉപകരണങ്ങളാണ് ഒരേ സമയം പ്രവർത്തിച്ചിരുന്നത്, അതും പരസ്പരം 3000 കിലോമീറ്റർ അകലത്തിൽ അമേരിക്കയിലെ രണ്ട് വ്യത്യസ്ത സംസ്ഥാനങ്ങളിൽ. ഇതിന് ഒരു കാരണം, എന്തെങ്കിലും സിഗ്നൽ ശ്രദ്ധയിൽ പെട്ടാൽ അത് സ്ഥിരീകരിക്കുന്നതിനുള്ള സൗകര്യമായിരുന്നു. ഉപകരണത്തിന്റെ സംവേദനക്ഷമത വച്ച് അടുത്തുകൂടി ഒരു ലോറിയോ മറ്റോ പോയാൽ പോലും ഇന്റർഫറൻസ് സിഗ്നൽ ഉണ്ടാകാൻ സാധ്യതയുണ്ട്. അത്തരം സിഗ്നലുകളെ ശല്യസിഗ്നലായി (noise) കണക്കാക്കും. ഇത്രയും അകലെയുള്ള രണ്ട് ഉപകരണങ്ങളിൽ ഒരേസമയം ഒരേ സിഗ്നൽ വന്നാൽ മാത്രമേ അത് പ്രസക്തമാകൂ. ഇത്രയും അകലെയുള്ള രണ്ടിലും ഒരേ ശല്യസിഗ്നൽ ഉണ്ടാകില്ലല്ലോ.
പിടി വീഴുന്നു...
ഇത്രയും സമീപഭൂതകാലത്തെ ശാസ്ത്രസാങ്കേതിക മുന്നേറ്റങ്ങളെ കുറിച്ചാണ് നാം സംസാരിച്ചത്. അടുത്തിടെ വാർത്തയിൽ കണ്ട സംഭവം സത്യത്തിൽ ആരംഭിച്ചത് ഇതിനൊക്കെ വളരെ മുൻപാണ്. മുൻപെന്ന് വച്ചാൽ, ഏതാണ്ട് 130 കോടി വർഷം മുൻപ്. അന്ന് LIGO-യും ഐൻസ്റ്റൈനും പോയിട്ട് മനുഷ്യരെന്ന ഹോമോ സാപിയൻസ് പോലും ഭൂമിയിൽ ഉണ്ടായിട്ടില്ല. അത്രയും പഴയ ഒരു ഫ്ലാഷ്-ബാക്ക് കാലത്ത്, രണ്ട് ബ്ലാക് ഹോളുകൾ തമ്മിൽ ഒരു കൂട്ടിയിടി നടന്നു. പരസ്പരം ചുറ്റിത്തിരിഞ്ഞ് ചുറ്റും ഗുരുത്വതരംഗങ്ങൾ പ്രവഹിപ്പിച്ച്, പതിയെപ്പതിയെ ഓർബിറ്റൽ ക്ഷയം സംഭവിച്ച് ഇവ ഒരുദിവസം അങ്ങ് കൂട്ടിയിടിക്കുകയാണ് ചെയ്തത്. അവയിൽ ഒന്നിന് സൂര്യന്റെ 29 മടങ്ങും മറ്റേതിന് 36 മടങ്ങും പിണ്ഡമുണ്ടായിരുന്നു. ഇവ കൂടിച്ചേർന്ന് സൂര്യനെക്കാൾ 62 മടങ്ങ് പിണ്ഡമുള്ള മറ്റൊരു പുതിയ ബ്ലാക് ഹോൾ ഉണ്ടായി. 29+36 എന്നത് 62 അല്ല. ഇവിടെ സൂര്യന്റെ മൂന്ന് മടങ്ങ് പിണ്ഡം കുറഞ്ഞിട്ടുണ്ട്. അത് മൊത്തം ഊർജമായി മാറി ഗുരുത്വതരംഗങ്ങളുടെ രൂപത്തിൽ പുറത്തേയ്ക്കൊഴുകി! (ഇത് ചില്ലറ ഊർജമൊന്നുമല്ല, ഒരു സെക്കൻഡിൽ പ്രപഞ്ചത്തിലെ എല്ലാ നക്ഷത്രങ്ങളും കൂടി ഉല്പാദിപ്പിക്കുന്ന ഊർജത്തിന്റെ 50 മടങ്ങ് വരും ഇത്.) പ്രപഞ്ചത്തിലൂടെ പ്രകാശവേഗതയിൽ പാഞ്ഞ ഈ തരംഗങ്ങൾ കഴിഞ്ഞ വർഷം സെപ്റ്റംബർ 14-നാണ് ഭൂമിയെ തഴുകി കടന്നുപോയത്. നമ്മുടെ രണ്ട് ലൈഗോ ഉപകരണങ്ങളിലും ഇവയുടെ കൈയൊപ്പ് പതിയുക തന്നെ ചെയ്തു. പക്ഷേ അത് കണ്ടയുടൻ ഓടിപ്പാഞ്ഞ് വന്ന് "ഞങ്ങ കണ്ടുപിടിച്ചേ" എന്ന് വിളിച്ചുകൂവുന്നത് സയൻസിന്റെ രീതിയല്ല. റെക്കോർഡ് ചെയ്യപ്പെട്ട സിഗ്നലിനെ സൂക്ഷ്മമായി പരിശോധിച്ച് കണ്ടെത്തിയത് ശരിയ്ക്കും നമ്മൾ കാണാനുദ്ദേശിച്ചത് തന്നെയാണ് എന്നുറപ്പിച്ച ശേഷമാണ് 2016 ഫെബ്രുവരിയിൽ ഔദ്യോഗികമായി ഇത് പ്രഖ്യാപിക്കപ്പെട്ടത്.
ശാസ്ത്രചരിത്രത്തിലെ നിർണായക നാഴികക്കല്ലുകളിൽ ഒന്നാണ് ഇത്. ഒരുപക്ഷേ ഗലീലിയോ 400 വർഷം മുൻപ് ആകാശത്തേയ്ക്ക് തന്റെ ടെലിസ്കോപ്പ് തിരിച്ചപ്പോൾ സംഭവിച്ചതുപോലൊരു വിപ്ലവം. ഇതുവരെ ഈ പ്രപഞ്ചത്തെക്കുറിച്ചുള്ള നമ്മുടെ അറിവിന്റെ ഏതാണ്ട് മൊത്തവും പ്രകാശം (വൈദ്യുതകാന്തിക തരംഗം) എന്ന ഒറ്റ സ്രോതസ്സിൽ നിന്നാണ് കിട്ടിയത്. എന്നാൽ പ്രകാശത്തിന് കടന്നുവരാനാകാത്ത സാഹചര്യങ്ങളിൽ പോലും അതുവഴി ഗുരുത്വതരംഗങ്ങൾക്ക് സഞ്ചരിക്കാനാകും. അതുകൊണ്ട് തന്നെ വൈദ്യുതകാന്തിക തരംഗങ്ങളെ നിരീക്ഷിക്കുന്നതിനോടൊപ്പം, ഗുരുത്വതരംഗങ്ങളെ കൂടി നിരീക്ഷിക്കാനായാൽ പ്രപഞ്ചത്തിലേയ്ക്കുള്ള ഒരു പുതിയ വാതിൽ തുറന്നിടലാകും അത്. ഇനിയും കൂടുതൽ സംവേദനക്ഷമതയുള്ള നിരീക്ഷണശാലകൾ സ്ഥാപിക്കാൻ നമ്മുടെ രാജ്യത്തുൾപ്പടെ പലയിടത്തും പദ്ധതികളുണ്ട്. ഇനിയും പിടികിട്ടാത്ത നിരവധി പ്രപഞ്ച രഹസ്യങ്ങൾ അതോടെ നമ്മുടെ മുന്നിൽ വെളിപ്പെട്ട് കിട്ടുമെന്നുറപ്പ്. Gravitational wave astronomy എന്നൊരു പുതിയ ശാഖ തന്നെ ഇതിനകം ഉണ്ടായിക്കഴിഞ്ഞു.
എന്തായാലും പ്രതീക്ഷിക്കാൻ ഇനിയും ഒരുപാടുണ്ട്. ഇതെല്ലാം കാണാനും കേൾക്കാനും ഐൻസ്റ്റൈൻ ഇല്ലാതായിപ്പോയല്ലോ എന്നൊരു സങ്കടമേയുള്ളൂ.










nice article...
ReplyDeleteThanks for the explanation
ReplyDelete